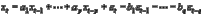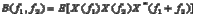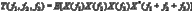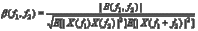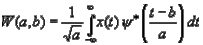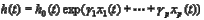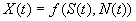omdec.com

By Daming Lin
Senior Technical Officer, Optimal Maintenance Decisions (OMDEC) Inc.
Extracted from Chapter 12 of “Reliability-centered Knowledge”

Introduction

In previous chapters we learned that Condition-based Maintenance recommends actions based on information acquired through observation and analysis. We noted, moreover, that the CBM process, itself contains three sub-processes or steps: data acquisiton, signal processing, and maintenance decision making.

Chapter 5. Case based reasoning (page 70) pointed out, in regard to complex systems, that prognostics are often indistinguishable from diagnostics, where both aim to identify the occurance of a potential failure.

Hundreds of theoretical and practical research papers on CBM appear every year in scientific journals, conference procedings and technical reports. In this chapter we provide an overview of recent developments in the diagnostics and prognostics of systems. We will mention a number of models, algorithms, and technologies for signal processing and maintenance decision making. Given the increased use of multiple sensors, we will also discuss various techniques for data fusion. The chapter is concluded with a brief discussion on current practices and possible future trends in CBM. The purpose of this survey of advanced methods of signal processing and decision making is not to instruct the reader in the the use of these new techniques, but merely to provide the maintenance professional with references to the source material so that he or she can investigate alternatives when encountering various situations where a CBM solution is proposed.

Reliability has always been an important criterion in the selection of industrial equipment. Good equipment design is essential for processes requiring high reliability. However, no amount of design effort will prevent deterioration over time. Machinery and systems operate under stress in an environment that is characterized by randomness. Maintenance is the major way in which we assure the user of the asset a satisfactory level of reliability. Physical asset managers look towards CBM as an efficient form of maintenance, which, they expect will assist them in the avoidance or reduction of risk. That is, they seek to reduce, to an acceptable level, the combined impact of the probability of failure and its consequences. A CBM program, if properly established and effectively implemented, can significantly reduce overall cost by reducing the number and/or extent of unnecessary preventive maintenance operations, while still achieving the desired reliability.

Let us begin by reviewing, briefly, the first CBM step, data acquisition.

Data acquistion

Data acquisition, the essential first step in the CBM task, is a process for collecting and storing useful information that emanates from operating physical assets. Data collected in a CBM program is of two main types: “event” data and condition monitoring (CM) data. Event data tells us what happened, for example, an installation, a breakdown, or an overhaul. Event data also tells us what was done, for example, a minor repair, a preventive maintenance action, an oil change, and so on. CM data consists of observational measurements that we believe are, in some way, related to the deteriorating health or state of the physical asset.

CM data can include vibration data, acoustics data, oil analysis data, temperature, pressure, moisture, humidity, and any other physical observations, including visual clues, that relate to to the condition of an operating physical asset in its environment. A variety of sensors (microsensors, ultrasonic sensors, acoustic emission sensors, thermographic imagers, etc) have been designed to collect different types of data [11,12]. Wireless technologies such as Bluetooth have provided an alternative to more expensive hard wired data communication. Information systems such as Computerized Maintenance Management Systems (CMMS), Enterprise Resource Planning (ERP) systems, control system historians, and CBM databases have been developed for data storage and handling[13]. With the rapid development of computer and advanced sensor technologies, data acquisition technologies have become more powerful and less expensive, resulting in exponentially growing databases of CM data.

Event data and CM data are equally important in CBM. In practice, however, engineers and managers tend to place more emphasis on the latter and sometimes neglect the former. Overlooking event data may have grown from the mistaken belief that it is not valuable to fault prediction as long as the condition monitoring data seems to be working well. We tend to overlook event data, in part, because we lack the knowledge and methods to use it. Event data is at least as helpful as CM data in assessing machine health. It augments our ability to judge the significance of CM data with respect to specific failure modes. The use of event data is discouraged by the fact that its collection usually implies manual data entry. Once a human is involved, everything becomes more complicated and error-prone. Choosing the “simple” solution, that of removing the human element, is hasty and ill-advised. Rather, as we discovered in Chapter 11. Information Procedures for Optimized CBM Policies (page 155), it is preferable to equip humans with tools and procedures with which to capture event data accurately, in a meaningful format, and in sufficient detail.

Signal processing

Under the topic of signal processing we include a necessary preliminary step - data cleaning. Data, especially event data, particularly when it is entered manually, always contains errors. Data cleaning is meant to ensure that clean (error-free) data is used for subsequent analysis and modeling. Data errors are caused by many factors, including the human factor mentioned previously. Errors in CM data may be caused by sensor faults, which are handled by sensor fault isolation[14]. In general, there is no simple, single method to clean data. Sometimes manual examination is required. Graphical tools are helpful in finding and removing data errors. Data cleaning is indeed a vast subject area. In Example 2 Data validation on page 129 (Chapter 10. ) we touched upon various aspects of data cleaning.

The next step in signal processing is data analysis. A variety of models, algorithms and tools are described in the technical literature. Their purpose is to analyze data in order to better understand and interpret it. The choice of which model, algorithm, or tool to use for data analysis depends primarily on the type of data collected. Condition monitoring data falls into three principal types:

Value: Data collected at a specific time epoch as single valued variables. For example, oil analysis data, temperature, pressure, humidity are all value type data.

Waveform: Data collected at a specific time epoch as a time series of values. For example, vibration data and acoustic data are or the waveform type.

Multi-dimension: Data collected at a specific time epoch as multi-dimensional values. The most common multi-dimensional data is image data, for example infrared thermographs, X-ray images, visual images, etc.

Although we have been using the term more broadly to describe the entire data analysis phase of CBM, “signal processing” usually refers most specifically to waveform and multi-dimension data analysis. A large variety of signal processing techniques have been developed to analyze and interpret these types of data. Their purpose is to extract useful information from the raw signal in order to perform diagnostics and prognostics. The signal processing procedure for extracting information relevant to targeted failure modes is often called “feature extraction”.

Signal processing

There are numerous signal processing techniques and algorithms in the literature for diagnostics and prognostics of mechanical systems. Case-dependent knowledge and investigation are required to select appropriate the signal processing tools from among a large number of possibilities.Waveform data analysis

The most common waveform data in condition monitoring are vibration signals and acoustic emissions. Other waveform data include ultrasonic signals, motor current, partial discharge, and others. In the literature, there are three main categories of waveform data analysis: time-domain analysis, frequency-domain analysis and time-frequency analysis.

Time-domain analysis is directly based on the time waveform itself. Traditional time-domain analysis calculates characteristic features from time waveform signals as descriptive statistics. For example: mean, peak, peak-to-peak interval, standard deviation, crest factor, high order statistics: RMS (root mean square), skewness, kurtosis, etc. These features are usually called time-domain features. A popular time-domain analysis approach is time synchronous average (TSA). The idea of TSA is to use the ensemble average of the raw signal over a number of evolutions in an attempt to remove or reduce noise and effects from other sources, so as to enhance the signal components of interest. A brief review of TSA was given by Dalpiaz[15] and some drawbacks of TSA were pointed out by Miller[16]. Most of the references on TSA can be found in [15,16].

More advanced approaches to time-domain analysis apply time series models to waveform data. The main idea of time series modeling is to fit the waveform data to a parametric time series model and extract features based on this parametric model. The popular models used in the literature are AR (autoregressive) model and ARMA (autoregressive moving average) model. An ARMA model of order() , denoted by ARMA(), is expressed by

where() is the waveform signal,() ’s are independent normally distributed with mean 0 and constant variance , and ()are model coefficients. An AR model of order() is a special case of ARMA() with (). Poyhonen et al[17] applied AR model to vibration signals collected from an induction motor and used the AR model coefficients as extracted features. Baillie and Mathew[18] compared the performance of three autoregressive time series modeling techniques: AR model, back propagation neural networks and radial basis function networks, to bearing fault diagnostics. Garga[19] proposed using AR modeling followed by dimension reduction for machinery fault diagnostics. Recently, Zhan[20] used a state space model representation of an AR model to analyze vibration signals for fault detection.

There are many other time-domain analysis techniques to analyze waveform data for machinery fault diagnostics. Some of them are briefly described as follows. Wang et al [21] introduced three nonlinear diagnostic methods for rotating machine fault diagnosis. These three methods are pseudo-phase portrait, singular spectrum analysis and correlation dimension. Pseudo-phase portrait is simple for computer execution and is sensitive to some fault types. Wang and Lin[22] used a statistical approach known as singular value decomposition to obtain the pseudo-phase portrait. Singular spectrum analysis can reveal the complexity of a signal and reduce the noise. Correlation dimension can provide some intrinsic information of an underlying dynamical system. Koizumi[23] also considered application of correlation dimension to fault diagnosis. Wang et al[24] applied both correlation dimension and bispectrum for rotating machine fault diagnosis. Zhuge and Lu[25] proposed a modified least mean square algorithm to model the non-stationary impulse-like signals for reciprocating machine fault diagnosis. Baydar et al investigated the use of a multivariate statistical technique known as principal component analysis (PCA) in gear fault diagnostics[26].

Frequency-domain analysis is based on the transformed signal in the frequency domain. The advantage of frequency-domain analysis over time-domain analysis is its ability to easily identify and isolate certain frequency components of interest. The most widely used conventional analysis is spectrum analysis by means of FFT (fast Fourier transform). The main idea of spectrum analysis is to either look at the whole spectrum or look closely at certain frequency components of interest and thus extract features from the signal (see, e.g.[27-29]). The most commonly used tool in spectrum analysis is the power spectrum. It is defined as() , where ()(and throughout this section) is the Fourier transform of signal (), E denotes expectation and “()” denotes complex conjugate. Some useful auxiliary tools for spectrum analysis are graphical presentation of the spectrum, frequency filters, envelope analysis (also called amplitude demodulation) [30-32], side band structure analysis [33], etc. Descriptions of the above mentioned techniques for FFT based spectrum can be found in textbooks such as[34,35] and will not be discussed in detail here. Another useful transform, Hilbert transform, has also been used for machine fault detection and diagnostics[30,36].

Despite the wide acceptance of the power spectrum, other useful spectra for signal processing have been developed and have been shown to have their own advantages over the FFT spectrum in certain cases. Cepstrum has the capability to detect harmonics and sideband patterns in the power spectrum. There are several versions or definitions of cepstrum[35]. Among them, the power cepstrum, which is defined as the inverse Fourier transform of the logarithmic power spectrum, is the most commonly used. A modified cepstrum analysis was proposed in[37]. A high order spectrum, i.e. bispectrum or trispectrum, can provide more diagnostic information than the power spectrum for non-Gaussian signals. In the literature, high order spectrum is also called high order statistics [38]. This name comes from the fact that bispectrum and trispectrum are actually the Fourier transforms of the third- and fourth-order statistics of the time waveform, respectively. But this name could be confused with the time-domain high order statistics. Bispectrum and trispectrum are defined as

and

respectively. Bispectrum and trispectrum can be normalized to obtain bicoherence and tricoherence as

and

respectively. Bispectrum analysis has been shown to have wide application in machinery diagnostics for various mechanical systems such as gears[39], bearings [40], rotating machines[41,42] and induction machines[43,24]. Li[44] investigated the application of bispectrum diagonal slice to gear fault diagnostics. Yang[40] used both bispectrum diagonal slice and bicoherence diagonal slice , summed bispectrum, and summed bicoherence for bearing fault diagnostics. Application of both bispectrum and trispectrum to bearing fault diagnostics was discussed in [45]. A new technique called holospectrum was introduced by Qu[46] to integrate all the information of phase, amplitude and frequency of a waveform signal. Application of holospectrum to machine fault diagnostics was studied in[47,48]. A review on holospectrum and its applications was given by Qu[49] (in Chinese).

Generally speaking, there are two classes of approaches for power spectrum estimation. The first covers the non-parametric approaches that estimate the autocorrelation sequence of the signal and subsequently apply a Fourier transform to the estimated autocorrelation sequence. For details, see[50]. The second class includes the parametric approaches that build a parametric model for the signal and then estimate power spectrum based on the fitted model. Among them, AR spectrum[51-53] and ARMA spectrum[54] based on AR model and ARMA model respectively are the two most commonly used parametric spectra for machinery fault diagnostics.

One limitation of frequency-domain analysis is its inability to handle non-stationary waveform signals, which are very common when machinery faults occur. Thus, time-frequency analysis, which investigates waveform signals in both time and frequency domain, has been developed for non-stationary waveform signals. Traditional time-frequency analysis uses time-frequency distributions, which represents the energy or power of waveform signals in two-dimensional functions of both time and frequency. Short-time Fourier transform (STFT, and also called spectrogram) [55,56] and Wigner-Ville distribution[57-60] are the most popular time-frequency distributions. Cohen[61] reviewed a class of time-frequency distributions which include spectrogram, Wigner-Ville distribution, Choi-Williams and others. The idea of spectrogram is to divide the whole waveform signal into segments with a short time window and then apply a Fourier transform to each segment. Spectrogram has some limitations in time-frequency resolution due to signal segmentation. It can be applied only to non-stationary signals with slow change in their dynamics. Bilinear transforms such as Wigner-Ville distribution are not based on signal segmentation and thus overcome the time-frequency resolution limitation of spectrogram. However, there is one main disadvantage of bilinear transforms, which is due to interference terms formed by the transformation itself. These interference terms make interpretation of the estimated distribution difficult[62]. Improved transforms such as the Choi-Williams distribution have been developed to overcome this difficulty. Gu et al[63] applied singular value decomposition to extract features from the time-frequency distribution. Loughlin[64] used a set of conditional time-frequency moments as characteristic features for fault diagnosis.

Another transform for time-frequency analysis is the wavelet transform. Wavelet theory has been rapidly developed in the past decade and has wide application[65]. A continuous wavelet transform is defined as

where ()is the waveform signal, ()is the scale parameter, ()is the time parameter and ()is a wavelet, which is a zero average oscillatory function centered around zero with a finite energy, and “()” denotes complex conjugate. Commonly used wavelets are Morlet, Mexican hat, Haar, etc. Similar to Fourier transform, the wavelet transform has its discrete form, which is obtained by discretizing ()and() , and expressing ()in discrete form. Similar to FFT, a fast wavelet transform is likewise available for the calculation.

Wavelet analysis of a waveform signal expresses the signal in a series of oscillatory functions with different frequencies at different times by dilations via the scale parameter and translations via the time parameter() . Similar to the power spectrum and the phase spectrum in Fourier analysis, a scalogram defined as ()and a wavelet phase spectrum defined as ()the phase angle of the complex variable() are used to interpret the signal. Wavelet transformation has been successfully applied to fault diagnostics of gears
[66,67], bearings[68,69] and other mechanical systems[70,71]. Dalpiaz and Rivola
[72] assessed and compared the effectiveness and reliability of wavelet transform to other vibration signal analysis techniques for fault detection and diagnostics. Baydar and Ball[73] applied wavelet transform to both acoustic signals and vibration signals for gear tooth fault diagnostic. Addison et al[74] investigated the use of low-oscillation complex wavelets, Mexican hat and Morlet wavelets, as feature detection tools. Wavelet analysis using Haar wavelet was considered in[75,76]. Miller[77] used a wavelet basis as a comb filter to decompose vibration signals for gear fault diagnostics. A graphical tool called wavelet polar maps to display wavelet amplitude and phase was proposed in[78] and was applied to gear fault diagnostics in[79]. Wavelet transform combined with Fourier transform to enhance feature extraction capability was proposed in[80]. A more advanced transform, known as wavelet packet transform, was studied and applied to machinery fault diagnostics in[81-83]. A new technique know as basis pursuit based on a general wavelet packet dictionary was applied to rolling element bearing fault diagnostics in[84]. It was shown that basis pursuit has some advantages over other commonly used wavelet analysis approaches. A recent review with more references on the applications of wavelet transform in machine condition monitoring and fault diagnostics was given in[85].

Image processing

Image processing is similar to but more complicated than waveform signal processing due to one more dimension involved. In practice, raw images are usually very complicated and immediate information for fault detection is unavailable. In these cases, image processing techniques must be powerful enough to extract useful features from raw images for fault diagnosis — see[86,87] for descriptions and discussions on image processing tools and algorithms. Image processing seems unnecessary when raw images provide sufficient and clear information under visual examination to identify patterns and detect faults. However, image processing can still help in extracting features for automatic fault detection in such situations. In addition to raw images obtained via data acquisition, some waveform processing techniques such as time-frequency analysis also produce images. In these situations, image processing can be combined with waveform processing to obtain better results.

A few examples of applying image processing techniques in condition monitoring and fault diagnosis and prognosis are as follows. Wang and MacFadden[88] applied image processing techniques to spectrograms for early gear fault detection and diagnostics. Utsumi et al[89] used a wavelet transform to analyze ferrographic images for bearing diagnosis. Heger and Pandit[90] considered a wavelet-based segmentation approach to image processing for the condition monitoring and fault diagnostics of grinding tools. Ellwein et al[91] combined image processing techniques with waveform power spectrum density to identify a region of interest (ROI) for fault discrimination enhancement.

Value type data analysis

Value type data includes both raw data obtained via data acquisition and feature values extracted from raw signals via signal processing. Value type data looks much simpler than waveform and image data. However, complexity lies in the correlation structure when the number of variables is large. Multivariate analysis techniques such as PCA and independent component analysis (ICA) are very useful to handle data with complicated correlation structure. For example, Stellman et al[92] applied PCA to spectroscopic data to monitor the condition of a lubricant in helicopter rotary gearboxes. Allgood and Upadhyaya[93] performed PCA on certain descriptive statistics for DC motor diagnostics and prognostics. ICA is an extension of PCA and will be discussed later. When the number of variables is large, dimension reduction techniques such as PCA and project pursuit can be used for data reduction. For a review on dimension reduction techniques, see[94]. An example of applying dimension reduction techniques for machine fault diagnostics is given in[19].

Trend analysis techniques such as regression analysis and time series model are commonly used techniques for analyzing value type data. For example, Grimmelius et al[95] developed a prototype condition monitoring and diagnostics system for compression refrigeration plants using a regression analysis model to predict healthy system behavior. Yang et al[96] established an ARMA model to extract features from on-line data for power equipment diagnosis. Sinhap[97] applied both polynomial regression and an ARMA model to predict the trend of vibration peak amplitude for turbine fault diagnostics and prognostics.

Data analysis combining event data and condition monitoring data

Data analysis for event data only is well known as “reliability analysis”, which fits the event data to a time between events probability distribution and uses the fitted distribution for further analysis. In condition-based maintenance, however, additional information — condition monitoring data, is available. It is beneficial to analyze event data and condition monitoring data together. This combined data analysis can be accomplished by building a mathematical model that describes the underlying mechanism of a fault or a failure. The model built on both event and condition monitoring data is the basis for maintenance decision support — diagnostics and prognostics, which will be discussed in the next section.

A time-dependent proportional hazards model (PHM) is suitable for analyzing both event and condition monitoring data together. It has a hazard function of the form

where() is a baseline hazard function, ()are covariates which are functions of time, and ()are coefficients. The baseline hazard function can be in non-parametric or parametric form. A commonly used parametric baseline hazard function is the Weibull hazard function, which is the hazard function of the Weibull distribution. A PHM with Weibull baseline hazard function is called Weibull PHM. Jardine et al[98] proposed using a Weibull PHM to analyze the aircraft and marine engine failure data together with the metal concentration measurements of the engine oil. An extension of PHM is the proportional intensity model (PIM), which adopts a stochastic process setting and assumes a similar form to the intensity function of the stochastic process. Vlok et al[99] studied the application of PIM to analyze failure and diagnostic measurement data from bearings.

In reliability centered maintenance (RCM)[100], the concept known as the “P-F interval” is used to describe failure patterns in condition monitoring. A P-F interval is the time interval between a potential failure (P), which is identified by a condition indicator, and a functional failure (F). A P-F interval is a useful concept with which to determine an appropriate interval for periodic condition monitoring. A condition monitoring interval is usually set to the P-F interval divided by an integer. In practice, however, it is usually difficult to quantify the P-F interval (see Chapter 9. The Elusive P-F Curve page 102). Goode et al[101] assumed two Weibull distributions for the P-F interval and the I-P interval, i.e. from machine installation to a potential failure. Using the statistical process control (SPC) methods on historical data, they separated each machine life cycle into two zones: a stable zone and a failure zone. They used the stable zone duration times to fit a Weibull distribution for the I-P interval. Similarly, they used the failure zone duration times to fit the Weibull distribution for the P-F interval. Based on these two fitted distributions combined with the condition monitoring process, machine prognosis was derived.

A hidden Markov model (HMM)[102,103] is another model for analyzing event and condition monitoring data together. A HMM consists of two stochastic processes: a Markov chain with a finite number of states describing an underlying failure mechanism, and an observation process that depends on the hidden state. Bunks et al [104] applied a HMM to analyze Westland helicopter data which consists of gearbox fault class information and vibration measurements surrounding the occurance of various faults. The fault classes were treated as states in the hidden Markov chain, whereas the vibration measurements were treated as realizations of the observation process. The trained HMM using lab test data was then applied to fault classification for a data set from an operating gearbox. Dong and He[105] proposed a more general model, hidden semi-Markov model (HSMM), for hydraulic pump diagnostics. It was shown that HSMM outperforms HMM in pump diagnostics.

Lin and Makis[106] proposed using a partially observable stochastic model to describe the underlying failure mechanism of a system undergoing condition monitoring. The proposed model is similar to that of a HMM but it has some distinguishing characteristics. One (failure) state is observable, whle the partially hidden state process is continuous in time. The observation process, however, is in discrete in time. These characteristics are more realistic in relation to actual condition monitoring processes. The model parameters were estimated using both event and condition monitoring data. The fitted model is used for subsequent diagnostics and prognostics. A fast recursive parameter estimation procedure for a partially observable stochastic model was given in[107].

Other models in the literature that can be used to analyze both event and condition monitoring data are models using the delay time concept[108] and stochastic process models such as a gamma process[109].

Maintenance decision support

The ultimate goal and final step of a CBM program is maintenance decision making. Sufficient and efficient decision support will result in maintenance personnel’s taking the “right” maintenance actions given the current known information. Jardine[110] reviewed and compared several commonly used CBM decision strategies. They included trend analysis that is rooted in statistical process control, expert systems, and neural networks. Wang and Sharp[111] discussed the decision aspect of CBM and reviewed the recent development in modeling CBM decision support.

Diagnostics

Machine fault diagnostics is a discovery procedure based on mapping information in the measurement space and/or features in the feature space to machine faults in the fault space. From an “RCM” perspective, a machine fault may or may not have immediate consequences. If a fault does not have immediate consequences, other than those necessary to diagnose and repair it, it is a potential failure. The diagnostic action following the detection of a potential failure will be a proactive activity, initiated, often, by a condition based maintenance process. A common example is an alarm generated by a “rule” applied to the data in a control system historian. Besides a potential failure, a diagnostic alarm may also expose an otherwise hidden functional failure, usually the failure of a protective or backup device. The failure of a hidden function has the immediate consequence that a “multiple” failure is, from that moment on, highly probable. This topic was developed in Failure Finding Intervals of Chapter 3. on page 38.

The diagnostic mapping process is also called pattern recognition. Traditionally, pattern recognition was a manual exercise, performed with the assistance of graphical tools such as a power spectrum graph, a phase spectrum graph, a cepstrum graph, an AR spectrum graph, a spectrogram, a wavelet scalogram, a wavelet phase graph, and so on. However, manual pattern recognition requires expertise in the specific area of the diagnostic application. It is slow and expensive requiring highly trained and skilled personnel. Therefore, automatic pattern recognition is highly desirable. This can be achieved by classification of signals based on the information and/or features extracted from the signals. In the following sections, different machine fault diagnostic approaches are discussed with emphasis on statistical approaches and artificial intelligent approaches. Machine diagnostics with emphasis on practical issues was discussed in[112]. Various topics in fault diagnosis with emphasis on model-based and artificial intelligence approaches were covered in a recent co-authored book[113].

Statistical approaches

A common method of fault diagnostics is to detect whether a specific fault is present or not based on the available condition monitoring information without intrusive inspection of the machine. This fault detection problem can be described as a hypothesis test problem with null hypothesis H0: Fault A is present, against alternative hypothesis H1: Fault A is not present. In a concrete fault diagnostic problem, hypotheses H0 and H1 are interpreted into an expression using specific models or distributions, or the parameters of a specific model or distribution. Test statistics are then constructed to summarize the condition monitoring information so as to be able to decide whether to accept the null hypothesis H0 or reject it. See[114-116] for some examples of using hypothesis testing for fault diagnosis. Recently, a framework for fault diagnosis, called structured hypothesis tests, was proposed for conveniently handling complicated multiple faults of different types[117].

A conventional approach, statistical process control, which was originally developed in quality control theory, has been well developed and widely used in fault detection and diagnostics. The principle of SPC is to measure the deviation of the current signal from a reference signal representing the normal condition to see whether the current signal is within the control limits or not. An example of using SPC for damage detection was discussed in[118].

Cluster analysis, as a multivariate statistical analysis method, is a statistical classification approach that groups signals into different fault categories on the basis of the similarity of the characteristics or features they possess. It seeks to minimize within-group variance and maximize between-group variance. The result of cluster analysis is a number of heterogeneous groups with homogeneous contents. There are substantial differences between the groups, but the signals within a single group are similar. Application of cluster analysis in machinery fault diagnosis was discussed in[119,120]. A natural way of signal grouping is based on certain distance measures or similarity measures between two signals. These measures are usually derived from certain discriminant functions in statistical pattern recognition[121]. Commonly used distance measures are Euclidean distance, Mahalanobis distance, Kullback-Leibler distance and Bayesian distance. See[122-125] for some examples of using these distance metrics for fault diagnostics. Ding et al[122] introduced a new distance metric called quotient distance for engine fault diagnosis. Pan et al[126] proposed an extended symmetric, the Itakura distance, for signals in time-frequency representations, for example the Wigner-Ville distributions. In addition to distance measures, the feature vector correlation coefficient is a similarity measure commonly used for signal classification in machinery fault diagnosis[125]. Many clustering algorithms are available for distinguishing the signal groups [127]. A commonly used algorithm in machine fault classification is the nearest neighbour algorithm that fuses the two closest groups into a new group and calculates the distance between two groups as the distance of the nearest neighbour in the two separate groups[128]. The boundary between two adjacent groups is determined by the discriminant function used. A piecewise linear discriminant function was used and thus piecewise linear boundaries were obtained for bearing condition classification in [129]. A technique called support vector machine (SVM) is usually employed to optimize a boundary curve in the sense that the distance of the closest point to the boundary curve is maximized. The support vector machine approach applied to machine fault diagnosis was considered in [17,130].

The hidden Markov model (HMM) described earlier can also be used for fault classification. Early applications of HMM in fault classification and diagnostics treated the real machine faulty states and the machine normal state as the hidden states of the HMM[104,131]. Two recent applications of HMM in fault classification assumed a HMM with hidden states having no physical meaning for two machine conditions (normal and faulty) [132,133]. The trained HMMs are then used to decode an observation for fault classification in a machine whose condition is unknown. Xu and Ge[134] presented an intelligent fault diagnosis system based on a hidden Markov model. Ye et al[135] considered the application of 2-dimension HMM based on time-frequency analysis for fault diagnosis.

Artificial intelligence approaches

Artificial intelligence (AI) techniques have been increasingly applied to machine diagnosis and have shown improved performance over conventional approaches. In the literature, two popular AI techniques for machine diagnosis are artificial neural networks (ANN) and expert systems (ES). Other AI techniques include fuzzy logic systems (FLS), fuzzy-neural networks (FNN), neural-fuzzy systems (NFS), and evolutionary algorithms (EA). A review of recent developments in applications of AI techniques for induction machine stator fault diagnostics was given by Siddique et al[136].

An artificial neural network is a computational model that mimics the human brain. It consists of simple processing elements connected together in a complex layer structure. The model approximates a complex nonlinear function with multi-input and multi-output. One processing element comprises a node and a weight. The artificial neural network learns the unknown function by adjusting its weights with observations of input and output. This process is usually called training of an artificial neural network. There are various neural network models. The feedforward neural network (FFNN) is the most widely used neural network structure in machine fault diagnosis[137-140]. A special FFNN, mulitlayer perceptron (MLP) with the back propagation (BP) training algorithm, is the most commonly used neural network model for pattern recognition and classification. Hence it is popular in machine fault diagnostics as well[140,141,142]. The BP neural networks, however, have two main limitations: 1) difficulty of determining the appropriate network structure and the number of nodes; 2) slow convergence of the training process.

A cascade correlation neural network (CCNN) does not require initial determination of the network structure and the number of nodes. CCNN can be used in cases where on-line training is preferable. Spoerre[143] applied CCNN to bearing fault classification and showed that CCNN can result in utilizing the minimum network structure for fault recognition with satisfactory accuracy. Other neural network models applied in machine diagnostics are radial basis function neural networks[18], recurrent neural networks[144,145] and counter propagation neural networks (CPNN)[146]. The above ANN models usually use supervised learning algorithms which require external input such as a priori knowledge about the target or desired output. For example, a common practice of training a neural network model is to use a set of experimental data with known (seeded) faults. This training process is supervised learning. In contrast to supervised learning, unsupervised learning does not require external input. An unsupervised neural network learns by itself using new information available. Wang and Too[38] applied unsupervised neural networks, a self-organizing map (SOM), and learning vector quantization (LVQ) to the detection of rotating machine faults. Tallam et al [147] proposed several self-commissioning and on-line training algorithms for FFNN applied particularly to electric machine fault diagnostics. Sohn et al[116] used an autoassociative neural network to separate the effect of damage on the extracted features from those caused by the environmental and vibration variations of the system. Then a sequential probability ratio test was performed on the normalized features for damage classification.

In contrast to neural networks, which acquire knowledge by training on observed data with known inputs and outputs, expert systems utilize domain expert knowledge in a computer program with an automated inference engine to perform reasoning for problem solving. Three main reasoning methods for ES used in the area of machinery diagnostics are rule-based reasoning[148-150], case-based reasoning[151,152] and model-based reasoning[153]. Another reasoning method, negative reasoning, was introduced to mechanical diagnosis by Hall et al[154]. Stanek et al[155] compared case-based and model-based reasoning and proposed to combine them for a lower cost solution to machine condition assessment and diagnosis. Unlike other reasoning methods, negative reasoning deals with negative information, which by its absence or lack of symptoms is indicative of meaningful inferences.

Expert systems and neural networks have known limitations. A significant limitation of rule-based expert systems is combinatorial explosion, which refers to the computation problem caused when the number rules increases exponentially as the number of variables increases. Another important limitation is consistency maintenance, which refers to the process by which the system decides when some of the variables need to be recomputed in response to changes in other values. Two important limitations of neural networks are the difficulty to have physical explanations of the trained model and the difficulty of the training process. It is natural then to attempt a combination of both techniques in order to combine their respective advantages thus improving performance in a hybrid system. For instance, Silva et al[156] used two neural networks, SOM and adaptive resonance theory (ART), combined with an expert system based on Taylor's tool life equation to classify tool wear state. DePold and Gass[157] studied the applications of neural networks and expert systems in a modular intelligent and adaptive system for gas turbine diagnostics and prognostics. Yang et al[158] presented an approach for integrating case-based reasoning ES with an ART-Kohonen neural network to enhance fault diagnosis. It was shown that the proposed approach outperforms the self-organizing feature map (SOFM) based system with respect to classification rate.

In condition monitoring practice, knowledge from domain specific experts is usually inexact. Therefore expert system reasoning on domain knowledge is often imprecise. Measures of the uncertainties in knowledge and reasoning are required in order that an ES may provide more robust problem solving capability. Commonly used uncertainty measures are probability, fuzzy member functions in fuzzy logic theory, and belief functions in belief networks theory. An example of applying fuzzy logic to machine fault classification was given in[159] to classify frequency spectra representing various rolling element bearing faults. A comparison between conventional rule-based expert systems and belief networks applied to machine diagnostics was given in[160]. Du and Yeung[161] introduced an approach called fuzzy transition probability, which combines transition probability (Markov process) as well as the fuzzy set, to monitoring progressive faults. The application of fuzzy logic is usually incorporated with other techniques such as neural networks and expert systems. For example, Zhang et al[162] developed a fuzzy neural network for fault diagnosis of rotary machines to improve the recognition rate of pattern recognition, especially in the case when sample data are similar. Lou and Loparo[125] employed an adaptive neural-fuzzy inference system as a diagnostic classifier for bearing fault diagnosis. Liu et al[163] applied fuzzy logic and expert systems to build a fuzzy expert system for bearing fault detection. Chang et al[164] built a system for decision making support in a power plant using both a rule-based ES and fuzzy logic.

Neural networks and expert systems have also been combined with other AI techniques to enhance machine diagnostic systems. Garga et al[165] proposed a hybrid reasoning approach combining neural network, fuzzy logic and expert systems to integrate domain knowledge and test operational data. Evolutionary algorithms[166], which mimic the natural evolution process of a population, have also been shown to have merit when applied to machine diagnostics. Genetic algorithms (GA) are the most widely used type of EA. Sampath et al[167] proposed a GA-based optimization approach to gas turbine diagnostics. Several examples of ANN incorporating GA and other EA algorithms for machine fault classification and diagnostics are[168-170]. Other approaches Another class of machine fault diagnostic approaches are the model-based approaches[171,172]. These approaches utilize physics specific, explicit mathematical models of the monitored machine. Based on this explicit model, residual generation methods such as Kalman filter, parameter estimation (or system identification), and parity relations are used to obtain signals, called residuals, which indicate fault presence in the machine. The residuals are evaluated to detect, isolate and identify the faut(s). This general procedure is illustrated in Figure 12‑2 . Model-based approaches can be more effective than other approaches if a correct and accurate model is built. However, explicit mathematical modeling may not be feasible for complex systems.
 

Various model-based diagnostic approaches have been applied to fault diagnosis of a variety of mechanical systems such as gearboxes[173,174], bearings[175-177], rotors[178,179], and cutting tools[180]. Bartelmus[181,182] used mathematical modeling and computer simulation to aid signal processing and interpretation. Hansen et al[183] proposed an approach to more robust diagnosis based on the fusion of sensor-based and model-based information. Vania and Pennacchi[184] developed some methods to measure the accuracy of the results obtained with model-based techniques aimed to identify faults in rotating machines. The information provided by these methods was shown to be very helpful to precise fault identification as well as an evaluation the confidence of the diagnostic decision.

Petri nets, as a general purpose graphical tool for describing relations existing between conditions and events[185], have been applied recently to machine fault detection and diagnostics. Propes[186] used a fuzzy Petri net to describe operating mode transition and to detect a mode change event for fault detection and diagnosis in complex systems. Yang[187] proposed a hybrid Petri-net modeling method coupled with fault-tree analysis and Kalman filtering for early failure detection and fault isolation. Yang et al[188] introduced an approach for integrating case-based reasoning with Petri net for fault diagnosis of induction motors. The integrated approach was shown to outperform the conventional case-base reasoning expert system.

Prognostics

Compared with diagnostics, the literature on prognostics is much smaller. There are two main prediction types in machine prognostics. The most obvious and widely used is the prediction of how much time is left before a failure occurs (or, one or more faults or “potential failures”) given the current machine condition and the past (and future) operating profile. The time left before observing a failure is usually called “remaining useful life” or RUL.

In many situations, especially when a fault or a failure has catastrophic consequences (e.g. nuclear power plant), it is desirable to predict the chance that a machine operates without a fault or a failure up to some future time (for example, the next inspection), given the machine’s current condition and its past operational profile. In the general maintenance context, the probability that a machine operates without fault until next inspection interval is a good reference in helping to determine whether or not the inspection interval is appropriate.

Most of the papers in the literature of machine prognostics discuss only the former type of prognostics, namely RUL estimation. Only a small number of papers address the second type of prognostics[106,189]. In the following sections, we discuss 1. RUL estimation, 2. prognostics that incorporate maintenance actions or policies, and 3. the determination of the appropriate condition monitoring interval.

Remaining useful life

RUL, also called remaining service life, residual life, or remnant life, refers to the time left before observing a failure, given the current machine age, its condition, and the past operation profile. Note here that the definition of failure is crucial to the interpretation of RUL. Although there is some controversy in current industrial practice, a formal definition of failure can be found in many reliability textbooks.

Prognosis, requires knowledge (or data) on the fault propagation process as well as knowledge (or data) on the failure mechanism. The fault propagation process is usually tracked by a trending or forecasting model for certain condition variables. There are two ways of describing the failure. The first assumes that failure depends on the condition variables (which reflect the actual fault level)and a predetermined boundary. The most commonly used failure definition in this case is simple: failure occurs when the fault reaches the predetermined level.

The second builds a model for the failure mechanism using available historical data. Various definitions of failure can be used. A failure can be defined as the event that the machine is operating at an unsatisfactory level (a partial failure); or, it can be a total functional failure when the machine cannot perform its intended function at all; or it can be a breakdown when the machine stops operating; or it can be the attainment of a potential failure condition defined in terms of acceptable risk. Similar to diagnosis, the prognostic methods fall into three main categories: statistical approaches, artificial intelligent approaches and model-based approaches.

Goode et al[101] used SPC to separate the whole machine life into two intervals, the I-P (Installation-Potential failure) interval in which the machine is running correctly and the P-F (Potential failure-Functional failure) in which the machine is running with a problem. Based on two Weibull distributions assumed for the I-P and P-F time intervals respectively, failure prediction was derived in the two intervals and the RUL was estimated. Yan et al[190] employed a logistic regression model to calculate the probability of failure for given condition variables and an ARMA time series model to trend the condition variables for failure prediction. A predetermined level of failure probability was used to estimate the RUL. Phelps et al[191] proposed to track sensor-level test-failure probability vectors instead of the physical system or sensor parameters for prognostics. A Kalman filter with an associated interacting multiple model (IMM) was used to perform the tracking.

Two statistical models in survival analysis, PHM and PIM, are useful tools for RUL estimation in combination with a trending model for the fault propagation process. Banjevic and Jardine[192] discussed RUL estimation for a Markov failure time process which includes a joint model of PHM and a Markov property for the covariate evolution as a special case. Vlok et al[99] applied PIM with covariate extrapolation to estimate bearing residual life. HMM, a stochastic process model discussed earlier, is also a powerful tool for RUL estimation[193,194]. Lin and Makis[195] introduced a partially observable continuous-discrete stochastic process model to describe the hidden evolution process of the machine state associated with the observation process. RUL estimation, as one of the prediction tasks, was generated by the model. Wang et al[109] proposed a stochastic process, called a “gamma process”, with hazard rate as the the residual life prediction criterion. The condition information considered was expert judgment based on vibration analysis. Wang[108] used the residual delay time concept and stochastic filtering theory to derive the residual life distribution.

AI techniques applied to RUL estimation have been considered by some researchers. Zhang and Ganesan[196] used self-organizing neural networks, for multivariable trending of the fault development, to estimate the residual life of a bearing system. Wang and Vachtsevanos[197] applied dynamic wavelet neural networks to predict the fault propagation process and estimate the RUL as the time left before the fault reaches a given value. Yam et al[198] applied a recurrent neural network for predicting the machine condition trend. Dong et al[199] utilized a grey model and a BP neural network to predict machine condition. Wang et al[200] compared the results of applying recurrent neural networks and neural-fuzzy inference systems to predict the fault damage propagation trend. Chinnam and Baruah[201] presented a neural-fuzzy approach to estimating RUL for the situation where neither failure data nor a specific failure definition model is available, but domain experts with strong experiential knowledge are on hand.

Model-based approaches to prognosis require specific failure mechanism knowledge and theory relevant to the monitored machine. Ray and Tangirala[202] used a nonlinear stochastic model of fatigue crack dynamics for real-time computation of the time-dependent damage rate and accumulation in mechanical structures. Li et al[203,204] introduced two defect propagation models via failure mechanism modeling for RUL estimation of bearings. Oppenheimer and Loparo[178] applied a physical model for predicting the machine condition in combination with a fault strengths-to-life model, based on a crack growth law, to estimate RUL. Chelidze and Cusumano [205] proposed a general method for tracking the evolution of a hidden damage process given a situation where a slowly evolving damage process is related to a fast, directly observable dynamic system. Luo et al[206] introduced an integrated prognostic process based on data from model-based simulations under nominal and degraded conditions. Kacprzynski et al[207] proposed fusing the physics of failure modeling with relevant diagnostic information for helicopter gear prognosis.

A different way of applying model-based approaches to prognosis is to derive the explicit relationship between the condition variables and the lifetimes (current lifetime and failure lifetime) via failure mechanism modeling. Two examples of research along this line are[208] for machines considered as energy processors subject to vibration monitoring and[209] for bearings with vibration monitoring. Lesieutre et al[210] developed a hierarchical modeling approach for system simulation to assess RUL. Engel et al[211] discussed some practical issues regarding accuracy, precision and confidence of the RUL estimates.

Prognostics incorporating maintenance policies

The aim of machine prognosis is to provide decision support for maintenance actions. As such, it is natural to include maintenance policies in the consideration of the machine prognostic process. This makes the situation more complicated since extra effort is needed to describe the nature of maintenance policies. We interest ourselves particularly in policies governing in the broad class of maintenance actions that we know as “CBM” and have set out to describe in this review. Compared to conventional maintenance, mathematical models applicable to the CBM scenario are much fewer [212]. See also[213] for more recent references on maintenance modeling.

The main idea of prognostics incorporating maintenance policies is to optimize the maintenance policies according to certain criteria such as risk, cost, reliability and availability. Risk is defined as the combination of failure probability and consequence. Usually, consequence can be measured by cost. In this case, the risk criterion is equivalent to the cost criterion. However, there are some cases, for example, critical equipment in a power plant, in which consequence cannot be estimated by cost. In these scenarios, probability or reliability criterion would be more appropriate. Since the cost criterion applies to most situations, it is not surprising that the literature in CBM optimization is dominated by cost-based CBM optimization. The consequence analysis technique discussed in[214] is a general risk evaluation tool for CBM optimization based on various kinds of criteria.

First, we consider completely observable systems. Wang [215] developed a CBM model based on a random coefficient growth model where the coefficients of the regression growth model are assumed to follow known distribution functions. The model was used to determine the optimal critical level and inspection interval in CBM in terms of a criterion of interest, which can be cost, downtime or reliability. In a series of works[216-218], a stochastic model — gamma process, was used to describe the deterioration process; the system was considered as failed if its condition jumps above a pre-set failure level; a sequential (or non-periodic) inspection interval was assumed. Grall et al [216] went on to assume a multi-level control-limit rule replacement policy and obtained the optimal thresholds and inspection scheduling by minimizing the expected maintenance cost per unit time. Castanier et al [217] assumed a multi-level control-limit rule repair/replacement policy and obtained optimal thresholds and inspection scheduling based on a cost criterion and an availability criterion as well. Dieulle et al[218] assumed a one-level replacement policy and a sequentially chosen inspection interval using a maintenance scheduling function, and obtained the optimal threshold and inspection scheduling by minimizing the global cost per unit time. Amari and McLaughlin[219] utilized a Markov chain to describe the CBM model for a deterioration system subject to periodic inspection. The optimal inspection frequency and maintenance threshold were found to maximize the system availability.

Berenguer et al[220] presented a CBM structure for continuously deteriorating multi-component systems, which allows cost savings by performing simultaneous maintenance actions. Barata et al[221] used Monte-Carlo simulation to model continuously monitored deteriorating systems, non-repairable single components or multi-component repairable systems. Then optimal degradation thresholds of maintenance intervention were found to minimize the expected total system cost over a given mission time by a direct search. Marseguerra et al[222] used GA to find the optimal thresholds in the previous work by simultaneously optimizing two typical objectives of interest, profit and availability. Hosseini et al[223] employed generalized stochastic Petri nets to represent a CBM model for a system subject to deterioration failures and Poisson failures. It was assumed that deterioration failures are restored by major repair and Poisson failures are restored by minimal repair. The optimal maintenance policy and inspection interval were then found to maximize system throughput.

We turn now to the consideration of partially observable systems. Ohnishi et al[224] applied a Markov decision process model for a discrete-time deterioration system to find the optimal replacement policy in which minimal repair is used to restore a failure if the decision is not to replace. Hontelez et al [225] formulated the decision process as a discrete Markov decision problem based on a continuous deterioration process to find the optimum maintenance policy with respect to cost. Aven [226] presented a counting process approach to determining the replacement policy minimizing the long run expected cost. Barbera et al[227] proposed a CBM model assuming that exponential failures with failure rate depend on the condition variables, and fixed inspection intervals. The optimal maintenance action was then found to minimize the long-run average cost of maintenance actions and failures. Barbera et al[228] extended the previous work to the case of two-unit series systems. Christer et al[229] used a state space model and the Kalman filter to predict the erosion condition of the inductors in an induction furnace conditional on the indirect measurements to date. Then a replacement cost model was developed to obtain the optimal replacement policy given all available information. Kumar and Westberg[230] proposed a reliability based approach for estimating the optimal maintenance time interval or the optimal threshold of the maintenance policy to minimize the total cost per unit time. The authors used PHM to identify the importance of monitored variables and a total time on test (TTT) plot to find the optimal solution. Makis and Jardine[231] established a CBM model using a Markov process to describe the evolution process of condition variables and a PHM to describe the failure mechanism which depends both on age and condition variables. This CBM model was further elaborated in[232]. The optimal replacement policy of the hazard control limit type was then determined by minimizing the long-run expected total cost per unit time. Makis et al[233] applied optimal stopping theory to find the replacement policy maximizing the total expected profit during the machine life where no assumption of monotonicity of the signal process is made. Makis and Jiang[234] presented a framework for CBM optimization based on a continuous-discrete stochastic model. The evolution of the hidden machine state was described by a continuous-time Markov process, and the condition monitoring process was described by a discrete-time observation stochastic process which depends on the hidden machine state. Then the optimal replacement policy was found to minimize the long run expected cost per unit time using optimal stopping theory. Wang[235] applied a stochastic recursive control model for CBM optimization based on the assumptions that the item monitored follows a two-period failure process with the first period of a normal life and the second, of a potential failure. A stochastic recursive filtering model was used to predict the residual, and then a decision model was established to recommend the optimal maintenance actions. The optimal condition monitoring intervals were determined by a hybrid of simulation and analytical analysis. Okumura and Okino[236] constructed a generalized condition-based maintenance model, in which residual life loss and replacement preparation lead-time are included. The optimal inspection time vector and warning level of the target maintained system under a constraint preventive replacement probability were obtained by minimizing the long-run average incurred cost per unit time. Barros et al[237] considered an optimal CBM policy for a two-unit parallel system of which unit-level monitoring information is imperfect and/or partial.

Condition monitoring interval

There are two broad types of condition monitoring: continuous and periodic. By continuous monitoring one continuously monitor (usually by mounted sensors) a machine and trigger a warning alarm whenever something wrong is detected. Two limitations of continuous monitoring are: 1) it is often expensive; 2) the continuous monitoring of raw signals produces large volumes of data, including noise, leading to difficult and inaccurate diagnostics. Periodic monitoring, therefore, is used due to its being more cost effective. Diagnostics from periodic monitoring are often more accurate due to the use of filtered and/or processed the data. Of course, the risk of periodic monitoring is the possibility of missing some failure events that occur between successive inspections ([34], p. 131).

An important issue relevant to periodic monitoring is the determination of the condition monitoring interval. Optimal design of the condition monitoring interval (or inspection interval) has been studied together with optimal threshold design in some of the works discussed in the previous section [215-219,223,230,235,236]. The following research works considered condition monitoring interval determination only. Christer and Wang[238] derived a simple model to find the optimal time for next inspection based upon the wear condition obtained up to current inspection. The criterion is to minimize the expected cost per unit time over the time interval between the current inspection and the next inspection time. Okumura[239] used a delay-time model to obtain the optimal sequential inspection intervals of a CBM policy for a deteriorating system by minimizing the long-run average cost per unit time. Goode et al[240] used the model developed in[101] to determine the length of the next condition monitoring interval for a given risk level. Wang[241] developed a model for optimal condition monitoring intervals based on the failure delay time concept and the conditional residual time concept. Condition monitoring is assumed to be performed at a fixed condition monitoring interval over the whole life and at a dynamic condition monitoring interval as well in the failure delay-time period realizing that more frequent monitoring might be needed in this later period. A hybrid of simulation and analytical procedure was used to find the optimal intervals based on one of five cost criterion functions.

Multiple sensor data fusion

For a complex system, a single sensor is limited in its capability of collecting enough data for accurate condition monitoring, fault diagnosis and prognosis. Multiple sensors are needed in order to do a better job. With the rapid development of computer science and advanced sensor technology, there has been an increasing trend in the use of multiple sensors for condition monitoring, fault diagnosis and prognosis. Data collected from different sensors may contain dissimilar partial information on the same machine’s condition. The problem is knowing how to combine all partial information obtained from different sensors for accurate machine diagnosis and prognosis. The solution to this problem is the subject of multisensor data fusion.

There are many techniques to multisensor data fusion. They can be grouped into three main approaches: (1) data-level fusion, (2) feature-level fusion, and (3) decision-level fusion. For more discussion on these three approaches, see[242,243]. Heger and Pandit [90] used a data-level fusion approach to fuse images obtained by multidirectional illumination to generate an image with a high degree of relevant information for grinding tool condition monitoring and fault diagnostics. Liu and Wang[244] briefly reviewed some applications of these three multisensor data fusion approaches to machine diagnosis and prognosis, and applied a feature-level fusion approach called Cascade-Correlation neural network for rotating imbalance diagnosis. Diagnostics based on the multisensor data fusion was shown to outperform diagnostics based on a single sensor. Wang and Wang[245] used a decision-level data fusion approach called Dempster-Shafer evidence theory for diesel engine fault diagnosis. Kozlowski et al[246] proposed a model-based approach to battery diagnostics using decision-level data fusion. Byington et al[247] explored the methods to fuse non-commensurate oil and vibration features for better gearbox fault diagnostics and prognostics. Mannan et al[248] applied a radial basis function neural network to fuse the features extracted from images of machined surfaces and acoustic signals generated during the machining process. The results were applied to the diagnostics of cutting tools. Hannah et al[249] discussed frameworks in data fusion applications for condition monitoring and diagnostic engineering. Data fusion combined with CBM optimization was studied in[250,251]. Assessment and evaluation of data and information fusion strategies were discussed in[252,253]. Wang and Wang[254] discussed the reliability and self-diagnosis of sensors in a multisensor data fusion diagnostic system.

In a mechanical system with multiple sensors installed, data collected from each sensor may be a complicated mixture of data from several sources. But only some of the sources are related to a particular machine condition of interest. The problem is to separate the various sources for better machine diagnosis and prognosis by fusing the observed multisensor data. The technique for solving this problem is known as blind source separation (BSS)[255]. Recently, BSS has received increasing attention in the area of machine fault diagnostics and prognostics. The general idea behind BSS is shown in Figure 12‑3. It is assumed that the source signals() , generated from () unknown independent sources, and the noise signals() , independent of the source signals, are combined together by an unknown mixing process. The mixed result is observed at the channel output as an ()-dimensional () signal . A formula for the mixing process can be written as

where() is generally a non-linear, time-dependent function. A commonly used form for the mixing process separates the signal and noise, i.e.,() . The objective of BSS is to find a separating function that is applied to the observed signals to obtain an estimate of the source signals .

In the literature, there are two categories of mixing process: instantaneous and convolutive mixing process. A mixing process is instantaneous if ()is a time-independent (memoryless) function, and convolutive otherwise. The convolutive mixing process is more common, especially for mechanical systems. The instantaneous mixing model is also called an “independent component analysis” (ICA) model, which is a natural extension of PCA. For a survey of ICA theory and methods, see[256]. Several authors applied ICA together with other signal processing techniques for condition monitoring and machine fault diagnosis[257-260]. Tian et al[261] used ICA in frequency domain and wavelet filtering for gearbox fault diagnostics. Zhang et al[262] studied ICA for partially blind source separation of diagnostic signals for bearing faults with prior knowledge. For a convolutive mixing process, BSS is more complicated. Gelle et al[263] compared two approaches, namely a temporal approach and a frequency approach, to solving the BSS problem of rotating machine signals for monitoring and diagnosis purposes. They further studied the application of the temporal approach to bearing fault diagnostics[264]. Tse and Zhang[265] applied the BSS based method of second order statistics to separate aggregated vibration signals generated from a number of mechanical components for machine fault diagnostics. Vilela et al[266] used the temporal de-correlation approach to separate the mixed acoustic signals for machine monitoring and fault diagnosis. Serviere et al[267] applied BSS to separate noisy harmonic signals for rotating machine diagnostics on a semi-blind mixing basis.

Concluding remarks

In this chapter, we have summarized recent research and developments in machinery diagnostics and prognostics used in implementing CBM. Various techniques, models and algorithms were reviewed. Of the three main steps of a CBM program, namely, data acquisition, signal processing, and maintenance decision making, we focused on the latter two. Finally we discussed various techniques for multiple sensor data fusion.

Although advanced maintenance techniques have been available in the literature, CBM, is under-employed by maintenance departments. Commercial predictive maintenance solution providers have not kept pace with recent advances in signal processing and decision support despite many situations, especially where both maintenance and failure are very costly, where well developed and managed condition-based maintenance is absolutely a better choice than current time based, or inadequate condition based, maintenance policies. Expert knowledge of both the application field and of reliability and maintenance theory are required for selecting and implementing effective condition based maintenance policies in each operating context.

Among the reasons that advanced maintenance technologies have not been well implemented in industry are: 1) lack of data due to incorrect data collecting approaches (see Chapter 11. page 155), 2) lack of efficient communication between theory developers and practitioners in the area of reliability and maintenance; 3) lack of efficient validation approaches; 4) difficulty of communication of the principles of CBM to business policy makers and management executives.

With the rapid development of the MEMS (micro-electro-mechanical systems) technology, future trends in CBM research will include the design of intelligent devices capable of continuously monitoring their own health (see, e.g.[268]). Fast and robust on-line signal processing algorithms are crucial to the design of intelligent devices. Such novel technology will, no doubt, stimulate increased research interest in this area. Another trend in CBM research is a growing collaboration among different, yet individually specialised, CBM research groups, for the joint devlopment of integrated platforms for enhanced diagnostics and prognostics (See[2] for an application of this idea).

References

[1] K. F. Martin, A Review by Discussion of Condition Monitoring and Fault-Diagnosis in Machine-Tools, International Journal of Machine Tools & Manufacture, 34 (1994) 527-551.

[2] J. Lee, R. Abujamra, A. K. S. Jardine, D. Lin, D. Banjevic, An integrated platform for diagnostics, prognostics and maintenance optimization, in: The IMS'2004 International Conference on Advances in Maintenance and in Modeling, Simulation and Intelligent Monitoring of Degradations, Arles, France, 2004.

[3] S. Nandi, H. A. Toliyat, Condition monitoring and fault diagnostic of electrical machines - a review, in: Thirty-Fourth IAS Annual Meeting, Vol. 1, Phoenix, AZ USA, 1999, pp. 197-204.

[4] H. C. Pusey, M. J. Roemer, Assessment of turbomachinery condition monitoring and failure prognosis technology, Shock and Vibration Digest, 31 (1999) 365-371.

[5] W. Q. Wang, F. Ismail, M. Farid Golnaraghi, Assessment of gear damage monitoring techniques using vibration measurements, Mechanical Systems and Signal Processing, 15 (2001) 905-922.

[6] M. Wang, A. J. Vandermaar, K. D. Srivastava, Review of condition assessment of power transformers in service, IEEE Electrical Insulation Magazine, 18 (2002) 12-25.

[7] A. El-Shafei, N. Rieger, Automated diagnostics of rotating machinery, in: 2003 ASME Turbo Expo, Vol. 4, Atlanta, GA, United States, 2003, pp. 491-498.

[8] T. K. Saha, Review of modern diagnostic techniques for assessing insulation condition in aged transformers, IEEE Transactions on Dielectrics and Electrical Insulation, 10 (2003) 903-917.

[9] R. M. Tallam, S. B. Lee, G. Stone, G. B. Kliman, J. Yoo, T. G. Habetler, R. G. Harley, A survey of methods for detection of stator related faults in induction machines, in: IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, Proceedings, New York, 2003, pp. 35-46.

[10] G. Sabnavis, R. G. Kirk, M. Kasarda, D. Quinn, Cracked shaft detection and diagnostics: a literature review, The Shock and Vibration Digest, 36 (2004) 287-296.

[11] H. Austerlitz, Data acquisition techniques using PCs, Academic Press, San Diego, Calif., 2003.

[12] N. V. Kirianaki, S. Y. Yurish, N. O. Shpak, V. P. Deynega, Data Acquisition and Signal Processing for Smart Sensors, John Wiley and Sons, Ltd., Chichester, West Sussex, England, 2002.

[13] C. Davies, R. M. Greenough, The use of information systems in fault diagnosis, in: Proceedings of the 16th National Conference on Manufacturing Research, University of East London, UK, 2000.

[14] R. Xu, C. Kwan, Robust isolation of sensor failures, Asian Journal of Control, 5 (2003) 12-23.

[15] G. Dalpiaz, A. Rivola, R. Rubini, Effectiveness and sensitivity of vibration processing techniques for local fault detection in gears, Mechanical Systems and Signal Processing, 14 (2000) 387-412.

[16] A. J. Miller, A New Wavelet Basis For The Decompostion Of Gear Motion Error Signals And Its Application To Gearbox Diagnostics, M.Sc. Thesis, Graduate Program in Acoustics, The Pennsylvania State University, State College, PA, 1999.

[17] S. Poyhonen, P. Jover, H. Hyotyniemi, Signal processing of vibrations for condition monitoring of an induction motor, in: ISCCSP : 2004 First International Symposium on Control, Communications and Signal Processing, New York, 2004, pp. 499-502.

[18] D. C. Baillie, J. Mathew, A comparison of autoregressive modeling techniques for fault diagnosis of rolling element bearings, Mechanical Systems and Signal Processing, 10 (1996) 1-17.

[19] A. K. Garga, B. T. Elverson, D. C. Lang, AR modeling with dimension reduction for machinery fault classification, in: Critical Link: Diagnosis to Prognosis, Haymarket, 1997, pp. 299-308.

[20] Y. Zhan, V. Makis, A. K. S. Jardine, Adaptive model for vibration monitoring of rotating machinery subject to random deterioration, Journal of Quality in Maintenance Engineering, 9 (2003) 351-375.

[21] W. J. Wang, J. Chen, X. K. Wu, Z. T. Wu, The application of some non-linear methods in rotating machinery fault diagnosis, Mechanical Systems and Signal Processing, 15 (2001) 697-705.

[22] W. J. Wang, R. M. Lin, The application of pseudo-phase portrait in machine condition monitoring, Journal of Sound and Vibration, 259 (2003) 1-16.

[23] T. Koizumi, N. Tsujiuchi, Y. Matsumura, Diagnosis with the correlation integral in time domain, Mechanical Systems and Signal Processing, 14 (2000) 1003-1010.

[24] W. J. Wang, Z. T. Wu, J. Chen, Fault identification in rotating machinery using the correlation dimension and bispectra, Nonlinear Dynamics, 25 (2001) 383-393.

[25] Q. Zhuge, Y. Lu, Signature analysis for reciprocating machinery with adaptive signal-processing, Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science, 205 (1991) 305-310.

[26] N. Baydar, Q. Chen, A. Ball, U. Kruger, Detection of incipient tooth defect in helical gears using multivariate statistics, Mechanical Systems and Signal Processing, 15 (2001) 303-321.

[27] R. R. Schoen, T. G. Habetler, Effects of time-varying loads on rotor fault detection in induction machines, IEEE Transactions on Industry Applications, 31 (1995) 900-906.

[28] R. G. T. De Almeida, S. A. Da Silva Vicente, L. R. Padovese, New technique for evaluation of global vibration levels in rolling bearings, Shock and Vibration, 9 (2002) 225-234.

[29] Z. Liu, X. Yin, Z. Zhang, D. Chen, W. Chen, Online rotor mixed fault diagnosis way based on spectrum analysis of instantaneous power in squirrel cage induction motors, IEEE Transactions on Energy Conversion, 19 (2004) 485-490.

[30] D. Ho, R. B. Randall, Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals, Mechanical Systems and Signal Processing, 14 (2000) 763-788.

[31] R. B. Randall, J. Antoni, S. Chobsaard, The relationship between spectral correlation and envelope analysis in the diagnostics of bearing faults and other cyclostationary machine signals, Mechanical Systems and Signal Processing, 15 (2001) 945-962.

[32] J. R. Stack, R. G. Harley, T. G. Habetler, An amplitude Modulation detector for fault diagnosis in rolling element bearings, IEEE Transactions on Industrial Electronics, 51 (2004) 1097-1102.

[33] G. W. Blankenship, R. Singh, Analytical solution for modulation sidebands associated with a class of mechanical oscillators, Journal of Sound and Vibration, 179 (1995) 13-36.

[34] S. Goldman, Vibration Spectrum Analysis : A Practical Approach, Industrial Press, New York, 1999.

[35] C. M. Harris, A. G. Piersol, Harris' Shock and Vibration Handbook, McGraw-Hill, 2002.

[36] M. A. Minnicino, H. J. Sommer, Detecting and quantifying friction nonlinearity using the Hilbert transform, in: Health Monitoring and Smart Nondestructie Evaluation of Structural and Biological System III, 5394, Bellingham, 2004, pp. 419-427.

[37] N. T. van der Merwe, A. J. Hoffman, A modified cepstrum analysis applied to vibrational signals, in: Proceedings of 14th International Conference on Digital Signal Processing (DSP2002), Vol. 2, Santorini, Greece, 2002, pp. 873-876.

[38] C.-C. Wang, G.-P. J. Too, Rotating machine fault detection based on HOS and artificial neural networks, Journal of Intelligent Manufacturing, 13 (2002) 283-293.

[39] L. Xiong, T. Shi, S. Yang, R. B. K. N. Rao, A novel application of wavelet-based bispectrum analysis to diagnose faults in gears, International Journal of COMADEM, 5 (2002) 31-38.

[40] D.-M. Yang, A. F. Stronach, P. Macconnell, J. Penman, Third-order spectral techniques for the diagnosis of motor bearing condition using artificial neural networks, Mechanical Systems and Signal Processing, 16 (2002) 391-411.

[41] T. W. S. Chow, G. Fei, Three phase induction machines asymmetrical faults identification using bispectrum, IEEE Transactions on Energy Conversion, 10 (1995) 688-693.

[42] N. Arthur, J. Penman, Inverter fed induction machine condition monitoring using the bispectrum, in: Proceedings of the IEEE Signal Processing Workshop on Higher-Order Statistics, Banff, Alta., Canada, 1997, pp. 67-71.

[43] B. E. Parker, H. A. Ware, D. P. Wipf, W. R. Tompkins, B. R. Clark, E. C. Larson, H. V. Poor, Fault diagnostics using statistical change detection in the bispectral domain, Mechanical Systems and Signal Processing, 14 (2000) 561-570.

[44] W. Li, G. Zhang, T. Shi, S. Yang, Gear crack early diagnosis using bispectrum diagonal slice, Chinese Journal of Mechanical Engineering (English Edition), 16 (2003) 193-196.

[45] A. C. McCormick, A. K. Nandi, Bispectral and trispectral features for machine condition diagnosis, IEE Proceedings-Vision, Image and Signal Processing, 146 (1999) 229-234.

[46] L. Qu, X. Liu, G. Peyronne, Y. Chen, The holospectrum: A new method for rotor surveillance and diagnosis, Mechanical Systems and Signal Processing, 3 (1989) 255-267.

[47] C. B. Yu, H. B. He, Y. Xu, F. L. Chen, Identification method of acoustic information flow of bearing state, in: Condition Monitoring '97, 1997, pp. 311-315.

[48] Y. D. Chen, R. Du, Diagnosing spindle defects using 4-D holospectrnm, Journal of Vibration and Control, 4 (1998) 717-732.

[49] L. Qu, D. Shi, Holospectrum during the past decade: review & prospect, Zhendong Ceshi Yu Zhenduan/Journal of Vibration, Measurement & Diagnosis, 18 (1998) 235-242 (in Chinese).

[50] M. H. Hayes, Statistical Digital Signal Processing and Modeling, John Wiley and Sons, New York, 1996.

[51] C. K. Mechefske, J. Mathew, Fault detection and diagnosis in low speed rolling element bearing. Part I: The use of parametric spectra, Mechanical Systems and Signal Processing, 6 (1992) 297-307.

[52] J. P. Dron, L. Rasolofondraibe, C. Couet, A. Pavan, Fault detection and monitoring of a ball bearing benchtest and a production machine via autoregressive spectrum analysis, Journal of Sound and Vibration, 218 (1998) 501-525.

[53] J. R. Stack, T. G. Habetler, R. G. Harley, Bearing fault detection via autoregressive stator current modeling, IEEE Transactions on Industry Applications, 40 (2004) 740-747.

[54] M. J. E. Salami, A. Gani, T. Pervez, Machine condition monitoring and fault diagnosis using spectral analysis techniques, in: Proceedings of the First International Conference on Mechatronics (ICOM '01), Vol. 2, Kuala Lumpar, Malaysia, 2001, pp. 690-700.

[55] W. J. Wang, P. D. McFadden, Early detection of gear failure by vibration analysis I. Calculation of the time-frequency distribution, Mechanical Systems and Signal Processing, 7 (1993) 193-203.

[56] F. A. Andrade, I. Esat, M. N. M. Badi, Gearbox fault detection using statistical methods, time-frequency methods (STFT and Wigner-Ville distribution) and harmonic wavelet - A comparative study, in: Proceedings of COMADEM '99, Chipping Norton, 1999, pp. 77-85.

[57] Q. Meng, L. Qu, Rotating machinery fault diagnosis using Wigner distribution, Mechanical Systems and Signal Processing, 5 (1991) 155-166.

[58] M.-C. Pan, H. Van Brussel, P. Sas, B. Verbeure, Fault diagnosis of joint backlash, Journal of Vibration and Acoustics, Transactions of the ASME, 120 (1998) 13-24.

[59] I. S. Koo, W. W. Kim, The development of reactor coolant pump vibration monitoring and a diagnostic system in the nuclear power plant, ISA Transactions, 39 (2000) 309-316.

[60] N. Baydar, A. Ball, A comparative study of acoustic and vibration signals in detection of gear failures using Wigner-Ville distribution, Mechanical Systems and Signal Processing, 15 (2001) 1091-1107.

[61] L. Cohen, Time-frequency distribution - a review, Proceedings of the IEEE, 77 (1989) 941-981.

[62] P. Bonato, R. Ceravolo, A. De Stefano, M. Knaflitz, Bilinear time-frequency transformations in the analysis of damaged structures, Mechanical Systems and Signal Processing, 11 (1997) 509-527.

[63] S. Gu, J. Ni, J. Yuan, Non-stationary signal analysis and transient machining process condition monitoring, International Journal of Machine Tools and Manufacture, 42 (2002) 41-51.

[64] P. Loughlin, F. Cakrak, L. Cohen, Conditional moments analysis of transients with application to helicopter fault data, Mechanical Systems and Signal Processing, 14 (2000) 511-522.

[65] R. K. Young, Wavelets Theory and Its Applications, Kluwer Academic Publishers, Boston, 1993.

[66] W. J. Staszewski, G. R. Tomlinson, Application of the wavelet transform to fault detection in a spur gear, Mechanical Systems and Signal Processing, 8 (1994) 289-307.

[67] W. J. Wang, P. D. McFadden, Application of wavelets to gearbox vibration signals for fault detection, Journal of Sound and Vibration, 192 (1996) 927-939.

[68] R. Rubini, U. Meneghetti, Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ball bearings, Mechanical Systems and Signal Processing, 15 (2001) 287-302.

[69] G. Y. Luo, D. Osypiw, M. Irle, On-line vibration analysis with fast continuous wavelet algorithm for condition monitoring of bearing, Journal of Vibration and Control, 9 (2003) 931-947.

[70] N. Aretakis, K. Mathioudakis, Wavelet analysis for gas turbine fault diagnostics, Journal of Engineering for Gas Turbines and Power, 119 (1997) 870-876.

[71] G. O. Chandroth, W. J. Staszewski, Fault detection in internal combustion engines using wavelet analysis, in: Proceedings of COMADEM '99, Chipping Norton, 1999, pp. 7-15.

[72] G. Dalpiaz, A. Rivola, Condition monitoring and diagnostics in automatic machines: comparison of vibration analysis techniques, Mechanical Systems and Signal Processing, 11 (1997) 53-73.

[73] N. Baydar, A. Ball, Detection of gear failures via vibration and acoustic signals using wavelet transform, Mechanical Systems and Signal Processing, 17 (2003) 787-804.

[74] P. S. Addison, J. N. Watson, T. Feng, Low-oscillation complex wavelets, Journal of Sound and Vibration, 254 (2002) 733-762.

[75] Y.-G. Xu, Y.-L. Yan, Research on Haar spectrum in fault diagnosis of rotating machinery, Applied Mathematics and Mechanics (English Edition), 12 (1991) 61-66.

[76] H. K. Tonshoff, X. Li, C. Lapp, Application of fast Haar transform and concurrent learning to tool-breakage detection in milling, IEEE/ASME Transactions on Mechatronics, 8 (2003) 414-417.

[77] A. J. Miller, K. M. Reichard, A new wavelet basis for automated fault diagnostics of gear teeth, in: Inter-Noise 99: Proceedings of the 1999 International Congress on Noise Control Engineering, Vol. 1-3, Poughkeepsie, 1999, pp. 1597-1602.

[78] D. Boulahbal, F. Golnaraghi, F. Ismail, Amplitude and phase wavelet maps for the detection of cracks in geared systems, Mechanical System and Signal Processing, 13 (1999) 423-436.

[79] G. Meltzer, N. P. Dien, Fault diagnosis in gears operating under non-stationary rotational speed using polar wavelet amplitude maps, Mechanical Systems and Signal Processing, 18 (2004) 985-992.

[80] C. Wang, R. X. Gao, Wavelet transform with spectral post-processing for enhanced feature extraction, IEEE Transactions on Instrumentation and Measurement, 52 (2003) 1296-1301.

[81] G. G. Yen, K.-C. Lin, Wavelet packet feature extraction for vibration monitoring, IEEE Transactions on Industrial Electronics, 47 (2000) 650-667.

[82] S. Zhang, J. Mathew, L. Ma, Y. Sun, Best basis-based intelligent machine fault diagnosis, Mechanical Systems and Signal Processing, 19 (2005) 357-370.

[83] H. A. Toliyat, K. Abbaszadeh, M. M. Rahimian, L. E. Olson, Rail defect diagnosis using wavelet packet decomposition, IEEE Transactions on Industry Applications, 39 (2003) 1454-1461.

[84] H. Yang, J. Mathew, L. Ma, Fault diagnosis of rolling element bearings using basis pursuit, Mechanical Systems and Signal Processing, 19 (2005) 341-356.

[85] Z. K. Peng, F. L. Chu, Application of the wavelet transform in machine condition monitoring and fault diagnostics: A review with bibliography, Mechanical Systems and Signal Processing, 18 (2004) 199-221.

[86] J. C. Russ, The Image Processing Handbook, CRC Press, Boca Raton, 2002.

[87] M. S. Nixon, A. S. Aguado, Feature Extraction and Image Processing, Newnes, Oxford, 2002.

[88] W. J. Wang, P. D. McFadden, Early detection of gear failure by vibration analysis II. Interpretation of the time-frequency distribution using image processing techniques, Mechanical Systems and Signal Processing, 7 (1993) 205-215.

[89] S. Utsumi, Z. Kawasaki, K. Matsu-Ura, M. Kawada, Use of wavelet transform and fuzzy system theory to distinguish wear particles in lubricating oil for bearing diagnosis, Electrical Engineering in Japan, 134 (2001) 36-44.

[90] T. Heger, M. Pandit, Optical wear assessment system for grinding tools, Journal of Electronic Imaging, 13 (2004) 450-461.

[91] C. Ellwein, S. Danaher, U. Jager, Identifying regions of interest in spectra for classification purposes, Mechanical Systems and Signal Processing, 16 (2002) 211-222.

[92] C. M. Stellman, K. J. Ewing, F. Bucholtz, I. D. Aggarwal, Monitoring the degradation of a synthetic lubricant oil using infrared absorption, fluorescence emission and multivariate analysis: A feasibility study, Lubrication Engineering, 55 (1999) 42-52.

[93] G. O. Allgood, B. R. Upadhyaya, A model-based high-frequency matched filter arcing diagnostic system based on principal component analysis (PCA) clustering, in: Applications and Science of Computational Intelligence III, 4055, Bellingham, 2000, pp. 430-440.

[94] I. K. Fodor, A Survey of Dimension Reduction Techniques, Lawrence Livermore National Laboratory (LLNL) Technical Report, UCRL-ID-148494, University of California, Livermore, CA, 2002.

[95] H. T. Grimmelius, J. K. Woud, G. Been, On-line failure diagnosis for compression refrigeration plants, International Journal of Refrigeration, 18 (1995) 31-41.

[96] L. Yang, M. Z. Yang, Z. Yan, B. Z. Shi, Extraction of symptom for on-line diagnosis of power equipment based on method of time series analysis, in: Proceedings of the 6th International Conference on Properties and Applications of Dielectric Materials, Vol. 1, Xi'an, China, 2000, pp. 314-317.

[97] B. K. Sinha, Trend prediction from steam turbine responses of vibration and eccentricity, Proceedings of the Institution of Mechanical Engineers Part A-Journal of Power and Energy, 216 (2002) 97-104.

[98] A. K. S. Jardine, P. M. Anderson, D. S. Mann, Application of the Weibull proportional hazard model to aircraft and marine engine failure data, Quality and Reliability Engineering International, 3 (1987) 77-82.

[99] P.-J. Vlok, M. Wnek, M. Zygmunt, Utilising statistical residual life estimates of bearings to quantify the influence of preventive maintenance actions, Mechanical Systems and Signal Processing, 18 (2004) 833-847.

[100] J. Moubray, Reliability-centred maintenance, Butterworth-Heinemann, Oxford, 1997.

[101] K. B. Goode, J. Moore, B. J. Roylance, Plant machinery working life prediction method utilizing reliability and condition-monitoring data, Proceedings of the Institution of Mechanical Engineers Part E-Journal of Process Mechanical Engineering, 214 (2000) 109-122.

[102] L. R. Rabiner, Tutorial on hidden Markov models and selected applications in speech recognition, Proceedings of the IEEE, 77 (1989) 257-286.

[103] R. J. Elliott, L. Aggoun, J. B. Moore, Hidden Markov Models: Estimation and Control, Springer-Verlag, New York, 1995.

[104] C. Bunks, D. McCarthy, T. Al-Ani, Condition-based maintenance of machines using Hidden Markov Models, Mechanical Systems and Signal Processing, 14 (2000) 597-612.

[105] M. Dong, D. He, Hidden semi-markov models for machinery health diagnosis and prognosis, in: Papers Presented at NAMRC 32, Vol. 32, Charlotte, NC, United States, 2004, pp. 199-206.

[106] D. Lin, V. Makis, Recursive filters for a partially observable system subject to random failure, Advances in Applied Probability, 35 (2003) 207-227.

[107] D. Lin, V. Makis, On-line parameter estimation for a failure-prone system subject to condition monitoring, Journal of Applied Probability, 41 (2004) 211-220.

[108] W. Wang, A model to predict the residual life of rolling element bearings given monitored condition information to date, IMA Journal of Management Mathematics, 13 (2002) 3-16.

[109] W. Wang, P. A. Scarf, M. A. J. Smith, On the application of a model of condition-based maintenance, Journal of the Operational Research Society, 51 (2000) 1218-1227.

[110] A. K. S. Jardine, Optimizing condition based maintenance decisions, in: Proceedings of the Annual Reliability and Maintainability Symposium, 2002, pp. 90-97.

[111] W. Wang, J. Sharp, Modelling condition-based maintenance decision support, in: Condition Monitoring: Engineering the Practice, Bury St Edmunds, 2002, pp. 79-98.

[112] J. H. Williams, A. Davies, P. R. Drake, Condition-based maintenance and machine diagnostics, Chapman & Hall, London, 1994.

[113] J. Korbicz, J. M. Koscielny, Z. Kowalczuk, W. Cholewa, Fault Diagnosis, Springer, Berlin, 2004.

[114] J. Ma, C. J. Li, Detection of Localized Defects in Rolling Element Bearings Via Composite Hypothesis Test, Mechanical Systems and Signal Processing, 9 (1995) 63-75.

[115] Y. W. Kim, G. Rizzoni, V. I. Utkin, Developing a fault tolerant power-train control system by integrating design of control and diagnostics, International Journal of Robust and Nonlinear Control, 11 (2001) 1095-1114.

[116] H. Sohn, K. Worden, C. R. Farrar, Statistical damage classification under changing environmental and operational conditions, Journal of Intelligent Material Systems and Structures, 13 (2002) 561-574.

[117] M. Nyberg, A general framework for fault diagnosis based on statistical hypothesis testing, in: Twelfth International Workshop on Principles of Diagnosis (DX 2001), Via Lattea, Italian Alps, 2001, pp. 135-142.

[118] M. L. Fugate, H. Sohn, C. R. Farrar, Vibration-based damage detection using statistical process control, Mechanical Systems and Signal Processing, 15 (2001) 707-721.

[119] V. A. Skormin, L. J. Popyack, V. I. Gorodetski, M. L. Araiza, J. D. Michel, Applications of cluster analysis in diagnostics-related problems, in: Proceedings of the 1999 IEEE Aerospace Conference, Vol. 3, Snowmass at Aspen, CO, USA, 1999, pp. 161-168.

[120] M. Artes, L. Del Castillo, J. Perez, Failure prevention and diagnosis in machine elements using cluster, in: Proceedings of the Tenth International Congress on Sound and Vibration, Stockholm, Sweden, 2003, pp. 1197-1203.

[121] J. Schurmann, Pattern Recognition: A Unified View of Statistical and Neural Approaches, John Wiley & Sons, New York, 1996.

[122] H. Ding, X. Gui, S. Yang, An approach to state recognition and knowledge-based diagnosis for engines, Mechanical Systems and Signal Processing, 5 (1991) 257-266.

[123] W. J. Staszewski, K. Worden, G. R. Tomlinson, Time-frequency analysis in gearbox fault detection using the Wigner-Ville distribution and pattern recognition, Mechanical Systems and Signal Processing, 11 (1997) 673-692.

[124] S. K. Goumas, M. E. Zervakis, G. S. Stavrakakis, Classification of washing machines vibration signals using discrete wavelet analysis for feature extraction, IEEE Transactions on Instrumentation and Measurement, 51 (2002) 497-508.

[125] X. Lou, K. A. Loparo, Bearing fault diagnosis based on wavelet transform and fuzzy inference, Mechanical Systems and Signal Processing, 18 (2004) 1077-1095.

[126] M.-C. Pan, P. Sas, H. Van Brussel, Machine condition monitoring using signal classification techniques, Journal of Vibration and Control, 9 (2003) 1103-1120.

[127] A. R. Webb, Statistical Pattern Recognition, John Wiley and Sons, West Sussex, England, 2002.

[128] C. K. Mechefske, J. Mathew, Fault detection and diagnosis in low speed rolling element bearing. Part II: The use of nearest neighbour classification, Mechanical Systems and Signal Processing, 6 (1992) 309-316.

[129] Q. Sun, P. Chen, D. Zhang, F. Xi, Pattern recognition for automatic machinery fault diagnosis, Journal of Vibration and Acoustics, Transactions of the ASME, 126 (2004) 307-316.

[130] M. Guo, L. Xie, S.-Q. Wang, J.-M. Zhang, Research on an integrated ICA-SVM based framework for fault diagnosis, in: Proceedings of the 2003 IEEE International Conference on Systems, Man and Cybernetics, Vol. 3, Washington, DC, USA, 2003, pp. 2710-2715.

[131] J. Ying, T. Kirubarajan, K. R. Pattipati, A. Patterson-Hine, A hidden Markov model-based algorithm for fault diagnosis with partial and imperfect tests, IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), 30 (2000) 463-473.

[132] M. Ge, R. Du, Y. Xu, Hidden Markov model based fault diagnosis for stamping processes, Mechanical Systems and Signal Processing, 18 (2004) 391-408.

[133] Z. Li, Z. Wu, Y. He, C. Fulei, Hidden Markov model-based fault diagnostics method in speed-up and speed-down process for rotating machinery, Mechanical Systems and Signal Processing, 19 (2005) 329-339.

[134] Y. Xu, M. Ge, Hidden Markov model-based process monitoring system, Journal of Intelligent Manufacturing, 15 (2004) 337-350.

[135] D. Ye, Q. Ding, Z. Wu, New method for faults diagnosis of rotating machinery based on 2-dimension hidden Markov model, in: Proceedings of the International Symposium on Precision Mechanical Measurement, Vol. 4, Hefei, China, 2002, pp. 391-395.

[136] A. Siddique, G. S. Yadava, B. Singh, Applications of artificial intelligence techniques for induction machine stator fault diagnostics: Review, in: Proceedings of the IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives, New York, 2003, pp. 29-34.

[137] M. J. Roemer, C. Hong, S. H. Hesler, Machine health monitoring and life management using finite element-based neural networks, Journal of Engineering for Gas Turbines and Power-Transactions of the ASME, 118 (1996) 830-835.

[138] E. C. Larson, D. P. Wipf, B. E. Parker, Gear and bearing diagnostics using neural network-based amplitude and phase demodulation, in: Proceedings of the 51st Meeting of the Society for Machinery Failure Prevention Technology, Virginia Beach, VA, 1997, pp. 511-521.

[139] B. Li, M.-Y. Chow, Y. Tipsuwan, J. C. Hung, Neural-network-based motor rolling bearing fault diagnosis, IEEE Transactions on Industrial Electronics, 47 (2000) 1060-1069.

[140] Y. Fan, C. J. Li, Diagnostic rule extraction from trained feedforward neural networks, Mechanical Systems and Signal Processing, 16 (2002) 1073-1081.

[141] B. A. Paya, I. I. Esat, M. N. M. Badi, Artificial neural network based fault diagnostics of rotating machinery using wavelet transforms as a preprocessor, Mechanical Systems and Signal Processing, 11 (1997) 751-765.

[142] B. Samanta, K. R. Al-Balushi, Artificial neural network based fault diagnostics of rolling element bearings using time-domain features, Mechanical Systems and Signal Processing, 17 (2003) 317-328.

[143] J. K. Spoerre, Application of the cascade correlation algorithm (CCA) to bearing fault classification problems, Computers in Industry, 32 (1997) 295-304.

[144] D. W. Dong, J. J. Hopfield, K. P. Unnikrishnan, Neural networks for engine fault diagnostics, in: Neural Networks for Signal Processing VII, New York, 1997, pp. 636-644.

[145] C. J. Li, T.-Y. Huang, Automatic structure and parameter training methods for modeling of mechanical systems by recurrent neural networks, Applied Mathematical Modelling, 23 (1999) 933-944.

[146] P. Deuszkiewicz, S. Radkowski, On-line condition monitoring of a power transmission unit of a rail vehicle, Mechanical Systems and Signal Processing, 17 (2003) 1321-1334.

[147] R. M. Tallam, T. G. Habetler, R. G. Harley, Self-commissioning training algorithms for neural networks with applications to electric machine fault diagnostics, IEEE Transactions on Power Electronics, 17 (2002) 1089-1095.

[148] Y. H. Yoon, E. S. Yoon, K. S. Chang, Process fault diagnostics using the integrated graph model, in: On-Line Fault Detection and Supervision in the Chemical Process Industries, Oxford, 1993, pp. 89-94.

[149] C. H. Hansen, R. K. Autar, J. M. Pickles, Expert systems for machine fault diagnosis, Acoustics Australia, 22 (1994) 85-90.

[150] M. F. Baig, N. Sayeed, Model-based reasoning for fault diagnosis of twin-spool turbofans, Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 212 (1998) 109-116.

[151] Z. Y. Wen, J. Crossman, J. Cardillo, Y. L. Murphey, Case base reasoning in vehicle fault diagnostics, in: Proceedings of the International Joint Conference on Neural Networks 2003, Vol. 1-4, New York, 2003, pp. 2679-2684.

[152] M. Bengtsson, E. Olsson, P. Funk, M. Jackson, Technical design of condition based maintenance system-a case study using sound analysis and case-based reasoning, in: Maintenance and Reliability Conference - Proceedings of the 8th Congress, Knoxville, USA, 2004.

[153] M. L. Araiza, R. Kent, R. Espinosa, Real-time, embedded diagnostics and prognostics in advanced artillery systems, in: 2002 IEEE Autotestcon Proceeedings, Systems Readiness Technology Conference, New York, 2002, pp. 818-841.

[154] D. L. Hall, R. J. Hansen, D. C. Lang, The negative information problem in mechanical diagnostics, Journal of Engineering for Gas Turbines and Power-Transactions of the Asme, 119 (1997) 370-377.

[155] M. Stanek, M. Morari, K. Frohlich, Model-aided diagnosis: An inexpensive combination of model-based and case-based condition assessment, IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews, 31 (2001) 137-145.

[156] R. G. Silva, R. L. Reuben, K. J. Baker, S. J. Wilcox, Tool wear monitoring of turning operations by neural network and expert system classification of a feature set generated from multiple sensors, Mechanical Systems and Signal Processing, 12 (1998) 319-332.

[157] H. R. DePold, F. D. Gass, The application of expert systems and neural networks to gas turbine prognostics and diagnostics, Journal of Engineering for Gas Turbines and Power, 121 (1999) 607-612.

[158] B.-S. Yang, T. Han, Y.-S. Kim, Integration of ART-Kohonen neural network and case-based reasoning for intelligent fault diagnosis, Expert Systems with Applications, 26 (2004) 387-395.

[159] C. K. Mechefske, Objective machinery fault diagnosis using fuzzy logic, Mechanical Systems and Signal Processing, 12 (1998) 855-862.

[160] G. C. Collins, J. R. Bourne, A. J. Brodersen, C. F. Lo, Comparison of rule-based and belief-based systems for diagnostic problems, in: Proceedings of The Second International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems (IEA/AIE - 89), Vol. 2, New York, USA, 1989, pp. 785-793.

[161] R. Du, K. Yeung, Fuzzy transition probability: A new method for monitoring progressive faults. Part 1: The theory, Engineering Applications of Artificial Intelligence, 17 (2004) 457-467.

[162] S. Zhang, T. Asakura, X. L. Xu, B. J. Xu, Fault diagnosis system for rotary machine based on fuzzy neural networks, JSME International Journal. Series C: Mechanical Systems, Machine Elements and Manufacturing, 46 (2003) 1035-1041.

[163] T. I. Liu, J. H. Singonahalli, N. R. Iyer, Detection of roller bearing defects using expert system and fuzzy logic, Mechanical Systems and Signal Processing, 10 (1996) 595-614.

[164] S. H. Chang, K. S. Kang, S. S. Choi, H. G. Kim, H. K. Jeong, C. U. Yi, Development of the on-line operator aid system OASYS using a rule-based expert system and fuzzy logic for nuclear power plants, Nuclear Technology, 112 (1995) 266-294.

[165] A. K. Garga, K. T. McClintic, R. L. Campbell, C. C. Yang, M. S. Lebold, T. A. Hay, C. S. Byington, Hybrid reasoning for prognostic learning in CBM systems, in: 2001 IEEE Aerospace Conference Proceedings, Vol. 1-7, New York, 2001, pp. 2957-2969.

[166] D. B. Fogel, An introduction to simulated evolutionary optimization, IEEE Transactions on Neural Networks, 5 (1994) 3-14.

[167] S. Sampath, S. Ogaji, R. Singh, D. Probert, Engine-fault diagnostics: an optimisation procedure, Applied Energy, 73 (2002) 47-70.

[168] Z. Y. Chen, Y. Y. He, F. L. Chu, J. Y. Huang, Evolutionary strategy for classification problems and its application in fault diagnostics, Engineering Applications of Artificial Intelligence, 16 (2003) 31-38.

[169] Y.-C. Huang, C.-M. Huang, Evolving wavelet networks for power transformer condition monitoring, IEEE Transactions on Power Delivery, 17 (2002) 412-416.

[170] G.-T. Yan, G.-F. Ma, Fault diagnosis of diesel engine combustion system based on neural networks, in: Proceedings of 2004 International Conference on Machine Learning and Cybernetics, Vol. 5, Shanghai, China, 2004, pp. 3111-3114.

[171] J. J. Gertler, Fault Detection and Diagnosis in Engineering Systems, Marcel Dekker, Inc., New York, 1998.

[172] S. Simani, C. Fantuzzi, R. J. Patton, Model-based Fault Diagnosis in Dynamic Systems Using Identification Techniques, Springer, London, 2003.

[173] I. Howard, S. Jia, J. Wang, The dynamic modelling of a spur gear in mesh including friction and a crack, Mechanical Systems and Signal Processing, 15 (2001) 831-838.

[174] W. Y. Wang, Towards dynamic model-based prognostics for transmission gears, in: Component and Systems Diagnostics, Prognostics, and Health Management II, 4733, Bellingham, 2002, pp. 157-167.

[175] D. C. Baillie, J. Mathew, Nonlinear model-based fault diagnosis of bearings, in: Proceedings of an International Conference on Condition Monitoring, Swansea, UK, 1994, pp. 241-252.

[176] K. A. Loparo, M. L. Adams, W. Lin, M. F. Abdel-Magied, N. Afshari, Fault detection and diagnosis of rotating machinery, IEEE Transactions on Industrial Electronics, 47 (2000) 1005-1014.

[177] K. A. Loparo, A. H. Falah, M. L. Adams, Model-based fault detection and diagnosis in rotating machinery, in: Proceedings of the Tenth International Congress on Sound and Vibration, Stockholm, Sweden, 2003, pp. 1299-1306.

[178] C. H. Oppenheimer, K. A. Loparo, Physically based diagnosis and prognosis of cracked rotor shafts, in: Component and Systems Diagnostics, Prognostics, and Health Management II, 4733, Bellingham, 2002, pp. 122-132.

[179] A. S. Sekhar, Model-based identification of two cracks in a rotor system, Mechanical Systems and Signal Processing, 18 (2004) 977-983.

[180] G. H. Choi, G. S. Choi, Application of minimum cross entropy to model-based monitoring in diamond turning, Mechanical Systems and Signal Processing, 10 (1996) 615-631.

[181] W. Bartelmus, Mathematical modelling and computer simulations as an aid to gearbox diagnostics, Mechanical Systems and Signal Processing, 15 (2001) 855-871.

[182] W. Bartelmus, Diagnostic information on gearbox condition for mechatronic systems, Transactions of the Institute of Measurement and Control, 25 (2003) 451-465.

[183] R. J. Hansen, D. L. Hall, S. K. Kurtz, A new approach to the challenge of machinery prognostics, Journal of Engineering for Gas Turbines and Power, 117 (1995) 320-325.

[184] A. Vania, P. Pennacchi, Experimental and theoretical application of fault identification measures of accuracy in rotating machine diagnostics, Mechanical Systems and Signal Processing, 18 (2004) 329-352.

[185] R. David, H. Alla, Petri nets for modeling of dynamic systems - a survey, Automatica, 30 (1994) 175-202.

[186] N. C. Propes, A fuzzy Petri net based mode identification algorithm for fault diagnosis of complex systems, in: System Diagnosis and Prognosis: Security and Condition Monitoring Issues III, 5107, Bellingham, 2003, pp. 44-53.

[187] S. K. Yang, A condition-based failure-prediction and processing-scheme for preventive maintenance, IEEE Transactions on Reliability, 52 (2003) 373-383.

[188] B.-S. Yang, S. K. Jeong, Y.-M. Oh, A. C. C. Tan, Case-based reasoning system with Petri nets for induction motor fault diagnosis, Expert Systems with Applications, 27 (2004) 301-311.

[189] C. R. Farrar, F. Hemez, G. Park, A. N. Robertson, H. Sohn, T. O. Williams, A Coupled Approach to Developing Damage Prognosis Solutions, in: Damage Assessment of Structures - The 5th International Conference on Damage Assessment of Structures (DAMAS 2003), Southampton, UK, 2003.

[190] J. Yan, M. Koc, J. Lee, A prognostic algorithm for machine performance assessment and its application, Production Planning and Control, 15 (2004) 796-801.

[191] E. Phelps, P. Willett, T. Kirubarajan, A statistical approach to prognostics, in: Component and Systems Diagnositics, Prognosis and Health Management, 4389, Bellingham, 2001, pp. 23-34.

[192] D. Banjevic, A. K. S. Jardine, Calculation of reliability function and remaining useful life for a Markov failure time process, To appear in IMA Journal of Management Mathematics, 2005.

[193] R. B. Chinnam, P. Baruah, Autonomous diagnostics and prognostics through competitive learning driven HMM-based clustering, in: Proceedings of the International Joint Conference on Neural Networks 2003, Vol. 1-4, New York, 2003, pp. 2466-2471.

[194] C. Kwan, X. Zhang, R. Xu, L. Haynes, A novel approach to fault diagnostics and prognostics, in: Proceedings of the 2003 IEEE International Conference on Robotics and Automation, Vol. 1-3, New York, 2003, pp. 604-609.

[195] D. Lin, V. Makis, Filters and parameter estimation for a partially observable system subject to random failure with continuous-range observations, Advances in Applied Probability, 36 (2004) 1212-1230.

[196] S. Zhang, R. Ganesan, Multivariable trend analysis using neural networks for intelligent diagnostics of rotating machinery, Transactions of the ASME. Journal of Engineering for Gas Turbines and Power, 119 (1997) 378-384.

[197] P. Wang, G. Vachtsevanos, Fault prognostics using dynamic wavelet neural networks, AI EDAM-Artificial Intelligence for Engineering Design Analysis and Manufacturing, 15 (2001) 349-365.

[198] R. C. M. Yam, P. W. Tse, L. Li, P. Tu, Intelligent predictive decision support system for condition-based maintenance, International Journal of Advanced Manufacturing Technology, 17 (2001) 383-391.

[199] Y.-L. Dong, Y.-J. Gu, K. Yang, W.-K. Zhang, A combining condition prediction model and its application in power plant, in: Proceedings of 2004 International Conference on Machine Learning and Cybernetics, Vol. 6, Shanghai, China, 2004, pp. 3474-3478.

[200] W. Q. Wang, M. F. Golnaraghi, F. Ismail, Prognosis of machine health condition using neuro-fuzzy systems, Mechanical Systems and Signal Processing, 18 (2004) 813-831.

[201] R. B. Chinnam, P. Baruah, A neuro-fuzzy approach for estimating mean residual life in condition-based maintenance systems, International Journal of Materials and Product Technology, 20 (2004) 166-179.

[202] A. Ray, S. Tangirala, Stochastic modeling of fatigue crack dynamics for on-line failure prognostics, IEEE Transactions on Control Systems Technology, 4 (1996) 443-451.

[203] Y. Li, S. Billington, C. Zhang, T. Kurfess, S. Danyluk, S. Liang, Adaptive prognostics for rolling element bearing condition, Mechanical Systems and Signal Processing, 13 (1999) 103-113.

[204] Y. Li, T. R. Kurfess, S. Y. Liang, Stochastic prognostics for rolling element bearings, Mechanical Systems and Signal Processing, 14 (2000) 747-762.

[205] D. Chelidze, J. P. Cusumano, A dynamical systems approach to failure prognosis, Journal of Vibration and Acoustics, 126 (2004) 2-8.

[206] J. Luo, A. Bixby, K. Pattipati, L. Qiao, M. Kawamoto, S. Chigusa, An interacting multiple model approach to model-based prognostics, in: System Security and Assurance, Vol. 1, Washington, DC, USA, 2003, pp. 189-194.

[207] G. J. Kacprzynski, A. Sarlashkar, M. J. Roemer, Predicting remaining life by fusing the physics of failure modeling with diagnostics, Journal of Metal, 56 (2004) 29-35.

[208] C. Cempel, H. G. Natke, M. Tabaszewski, A passive diagnostic experiment with ergodic properties, Mechanical Systems and Signal Processing, 11 (1997) 107-117.

[209] J. Qiu, C. Zhang, B. B. Seth, S. Y. Liang, Damage mechanics approach for bearing lifetime prognostics, Mechanical Systems and Signal Processing, 16 (2002) 817-829.

[210] G. A. Lesieutre, L. Fang, U. Lee, Hierarchical failure simulation for machinery prognostics, in: Critical Link: Diagnosis to Prognosis, Haymarket, 1997, pp. 103-110.

[211] S. J. Engel, B. J. Gilmartin, K. Bongort, A. Hess, Prognostics, the real issues involved with predicting life remaining, in: 2000 IEEE Aerospace Conference Proceedings, Vol. 6, New York, 2000, pp. 457-469.

[212] P. A. Scarf, On the application of mathematical models in maintenance, European Journal of Operational Research, 99 (1997) 493-506.

[213] D. Lugtigheid, D. Banjevic, A. K. S. Jardine, Modelling repairable system reliability with explanatory variables and repair and maintenance actions, IMA Journal Management Mathematics, 15 (2004) 89-110.

[214] J. E. Campbell, B. M. Thompson, L. P. Swiler, Consequence analysis in predictive health monitoring systems, in: Proceedings of Probabilistic Safety Assessment and Management, Vol. I and II, Amsterdam, 2002, pp. 1353-1358.

[215] W. Wang, A model to determine the optimal critical level and the monitoring intervals in condition-based maintenance, International Journal of Production Research, 38 (2000) 1425-1436.

[216] A. Grall, C. Berenguer, L. Dieulle, A condition-based maintenance policy for stochastically deteriorating systems, Reliability Engineering & System Safety, 76 (2002) 167-180.

[217] B. Castanier, C. Berenguer, A. Grall, A sequential condition-based repair/replacement policy with non-periodic inspections for a system subject to continuous wear, Applied Stochastic Models in Business and Industry, 19 (2003) 327-347.

[218] L. Dieulle, C. Berenguer, A. Grall, M. Roussignol, Sequential condition-based maintenance scheduling for a deteriorating system, European Journal of Operational Research, 150 (2003) 451-461.

[219] S. V. Amari, L. McLaughlin, Optimal design of a condition-based maintenance model, in: Proceedings of the Annual Reliability and Maintainability Symposium, Los Angeles, CA, USA, 2004, pp. 528-533.

[220] C. Berenguer, A. Grall, B. Castanier, Simulation and evaluation of condition-based maintenance policies for multi-component continuous-state deteriorating systems, in: Foresight and Precaution, Vol. 1-2, Rotterdam, 2000, pp. 275-282.

[221] J. Barata, C. G. Soares, M. Marseguerra, E. Zio, Simulation modelling of repairable multi-component deteriorating systems for 'on condition' maintenance optimisation, Reliability Engineering and System Safety, 76 (2002) 255-264.

[222] M. Marseguerra, E. Zio, L. Podofillini, Condition-based maintenance optimization by means of genetic algorithms and Monte Carlo simulation, Reliability Engineering and System Safety, 77 (2002) 151-165.

[223] M. M. Hosseini, R. M. Kerr, R. B. Randall, An inspection model with minimal and major maintenance for a system with deterioration and Poisson failures, IEEE Transactions on Reliability, 49 (2000) 88-98.

[224] M. Ohnishi, T. Morioka, T. Ibaraki, Optimal minimal-repair and replacement problem of discrete-time Markovian deterioration system under incomplete state information, Computers and Industrial Engineering, 27 (1994) 409-412.

[225] J. A. M. Hontelez, H. H. Burger, D. J. D. Wijnmalen, Optimum condition-based maintenance policies for deteriorating systems with partial information, Reliability Engineering and System Safety, 51 (1996) 267-274.

[226] T. Aven, Condition based replacement policies-a counting process approach, Reliability Engineering and System Safety, 51 (1996) 275-281.

[227] F. Barbera, H. Schneider, P. Kelle, A condition based maintenance model with exponential failures and fixed inspection intervals, Journal of the Operational Research Society, 47 (1996) 1037-1045.

[228] F. Barbera, H. Schneider, E. Watson, A condition based maintenance model for a two-unit series system, European Journal of Operational Research, 116 (1999) 281-290.

[229] A. H. Christer, W. Wang, J. M. Sharp, A state space condition monitoring model for furnace erosion prediction and replacement, European Journal of Operational Research, 101 (1997) 1-14.

[230] D. Kumar, U. Westberg, Maintenance scheduling under age replacement policy using proportional hazards model and TTT-plotting, European Journal of Operational Research, 99 (1997) 507-515.

[231] V. Makis, A. K. S. Jardine, Optimal replacement in the proportional hazards model, INFOR, 30 (1992) 172-183.

[232] D. Banjevic, A. K. S. Jardine, V. Makis, M. Ennis, A control-limit policy and software for condition-based maintenance optimization, INFOR, 39 (2001) 32-50.

[233] V. Makis, X. Jiang, A. K. S. Jardine, A condition-based maintenance model, IMA Journal of Mathematics Applied in Business and Industry, 9 (1998) 201-210.

[234] V. Makis, X. Jiang, Optimal replacement under partial observations, Mathematics of Operations Research, 28 (2003) 382-394.

[235] W. B. Wang, A stochastic control model for on line condition based maintenance decision support, in: 6th World Multiconference on Systemics, Cybernetics and Informatics, Vol. VI, Proceedings - Industrial Systems and Engineering I, Orlando, 2002, pp. 370-374.

[236] S. Okumura, N. Okino, Optimisation of inspection time vector and warning level in CBM considering residual life loss and constraint on preventive replacement probability, International Journal of COMADEM, 6 (2003) 10-18.

[237] A. Barros, A. Grall, C. Berenguer, A maintenance policy optimized with imperfect and/or partial monitoring, in: Proceedings of the Annual Reliability and Maintainability Symposium, New York, 2003, pp. 406-411.

[238] A. H. Christer, W. Wang, A simple condition monitoring model for a direct monitoring process, European Journal of Operational Research, 82 (1995) 258-269.

[239] S. Okumura, An inspection policy for deteriorating processes using delay-time concept, International Transactions in Operational Research, 4 (1997) 365-375.

[240] K. B. Goode, B. J. Roylance, J. Moore, Development of model to predict condition monitoring interval times, Ironmaking and Steelmaking, 27 (2000) 63-68.

[241] W. Wang, Modelling condition monitoring intervals: A hybrid of simulation and analytical approaches, Journal of the Operational Research Society, 54 (2003) 273-282.

[242] D. L. Hall, J. Llinas, Handbook of Multisensor Data Fusion, CRC Press, Boca Raton, FL, 2001.

[243] D. L. Hall, S. A. H. McMullen, Mathematical techniques in multi-sensor data fusion, Artech House, Boston, 2004.

[244] Q. Liu, H.-P. Wang, A case study on multisensor data fusion for imbalance diagnosis of rotating machinery, (AI EDAM) Artificial Intelligence for Engineering Design, Analysis and Manufacturing, 15 (2001) 203-210.

[245] H. F. Wang, J. P. Wang, Fault diagnosis theory: method and application based on multisensor data fusion, Journal of Testing and Evaluation, 28 (2000) 513-518.

[246] J. D. Kozlowski, C. S. Byington, A. K. Garga, M. J. Watson, T. A. Hay, Model-based predictive diagnostics for electrochemical energy sources, in: 2001 IEEE Aerospace Conference, Vol. 6, Big Sky, MT, 2001, pp. 63149-63164.

[247] C. S. Byington, T. A. Merdes, J. D. Kozlowski, Fusion techniques for vibration and oil debris/quality in gearbox failure testing, in: Proceedings of Condition Monitoring '99, Chipping Norton, 1999, pp. 113-128.

[248] M. A. Mannan, A. A. Kassim, M. Jing, Application of image and sound analysis techniques to monitor the condition of cutting tools, Pattern Recognition Letters, 21 (2000) 969-979.

[249] P. Hannah, A. Starr, P. Bryanston-Cross, Condition monitoring and diagnostic engineering - A data fusion approach, in: Condition Monitoring and Diagnostic Engineering Management, Amsterdam, 2001, pp. 275-282.

[250] R. Willetts, A. G. Starr, D. Banjevic, A. K. S. Jardine, A. Doyle, Optimising complex CBM decisions using hybrid fusion methods, in: Condition Monitoring and Diagnostic Engineering Management, Amsterdam, 2001, pp. 909-918.

[251] A. Starr, R. Willetts, P. Hannah, W. Hu, D. Banjevic, A. K. S. Jardine, Data fusion applications in intelligent condition monitoring, in: Recent Advances in Computers, Computing and Communications, 2002, pp. 110-115.

[252] M. J. Roemer, G. J. Kacprzynski, R. F. Orsagh, Assessment of data and knowledge fusion strategies for prognostics and health management, in: 2001 IEEE Aerospace Conference Proceedings, Vol. 6, Big Sky, MT, USA, 2001, pp. 2979-2988.

[253] Z. B. Zhang, J. Wang, Y. Tian, H. Q. Zheng, Assessment of information fusion strategies for diagnostics and prognostics, in: Proceedings of ISTM/2003: 5th International Symposium on Test and Measurement, Vol. 1-6, Beijing, 2003, pp. 1901-1903.

[254] J. P. Wang, H. F. Wang, The reliability and self-diagnosis of sensors in a multisensor data fusion diagnostic system, Journal of Testing and Evaluation, 31 (2003) 370-377.

[255] S. S. Haykin, Unsupervised Adaptive Filtering, John Wiley and Sons, New York, 2000.

[256] A. Hyvarinen, Survey on independent component analysis, Neural Computing Surveys, 2 (1999) 94-128.

[257] L. Li, L. Qu, Machine diagnosis with independent component analysis and envelope analysis, in: International Conference on Industrial Technology: `Productivity Reincarnation through Robotics and Automation', Vol. 2, Bankok, Thailand, 2002, pp. 1360-1364.

[258] J. P. Barnard, C. Aldrich, Diagnostic monitoring of internal combustion engines by use of independent component analysis and neural networks, in: 2003 International Joint Conference on Neural Networks, Vol. 2, Portland, OR, USA, 2003, pp. 869-872.

[259] Z. S. Chen, Y. M. Yang, G. J. Shen, X. S. Wen, Early diagnosis of helicopter gearboxes based on independent component analysis, in: Proceedings of ISTM/2003: 5th International Symposium on Test and Measurement, Vol. 1-6, Beijing, 2003, pp. 3383-3386.

[260] X. J. Ma, Z. H. Hao, Mulltisensor data fusion based on independent component analysis for fault diagnosis of rotor, in: Advances in Neural Networks - ISNN 2004, Pt 1, 3173, Berlin, 2004, pp. 744-749.

[261] X. H. Tian, J. Lin, K. R. Fyfe, M. J. Zuo, Gearbox fault diagnosis using independent component analysis in the frequency domain and wavelet filtering, in: Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. II, Speech II; Industry Technology Tracks; Design and Implementation of Signal Processing Systems; Neural Networks for Signal Processing, New York, 2003, pp. 245-248.

[262] H. J. Zhang, L. S. Qu, B. G. Xu, G. G. Wen, Partially blind source separation of the diagnostic signals with prior knowledge, in: Condition Monitoring and Diagnostic Engineering Management, Amsterdam, 2001, pp. 177-184.

[263] G. Gelle, M. Colas, C. Serviere, BSS for fault detection and machine monitoring - time or frequency domain approach?, in: Proceedings of International Workshop on Independent Component Analysis and Blind Signal Separation (ICA 2000), Helsinki, Finland, 2000, pp. 555-560.

[264] G. Gelle, M. Colas, C. Serviere, Blind source separation: a new pre-processing tool for rotating machines monitoring?, IEEE Transactions on Instrumentation and Measurement, 52 (2003) 790-795.

[265] P. W. Tse, J. Zhang, The use of blind-source-separation algorithm for mechanical signal separation and machine fault diagnosis, in: 2003 ASME International Mechanical Engineering Congress, Vol. 24, Washington, DC., United States, 2003, pp. 57-63.

[266] R. M. Vilela, J. C. Metrolho, J. C. Cardoso, Machine and industrial monitorization system by analysis of acoustic signatures, in: Proceedings of the 12th IEEE Mediterranean Electrotechnical Conference (MELECON 2004), Vol. 1, Dubrovnik, Croatia, 2004, pp. 277-279.

[267] C. Serviere, P. Fabry, Blind source separation of noisy harmonic signals for rotating machine diagnosis, Journal of Sound and Vibration, 272 (2004) 317-339.

[268] F. M. Discenzo, P. J. Unsworth, K. A. Loparo, H. Marcy, Self-diagnosing intelligent motors: a key enabler for next generation manufacturing systems, IEE Colloquium (Digest), (1999) 15-18 (3/1-3/4).